Nastia Plays with a Tree

Description:

Input:

The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10\,000$$$) — the number of test cases.

The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 10^5$$$) — the number of vertices in the tree.

Next $$$n - 1$$$ lines of each test cases describe the edges of the tree in form $$$a_i$$$, $$$b_i$$$ ($$$1 \le a_i, b_i \le n$$$, $$$a_i \neq b_i$$$).

It's guaranteed the given graph is a tree and the sum of $$$n$$$ in one test doesn't exceed $$$2 \cdot 10^5$$$.

Output:

For each test case in the first line print a single integer $$$k$$$ — the minimum number of operations required to obtain a bamboo from the initial tree.

In the next $$$k$$$ lines print $$$4$$$ integers $$$x_1$$$, $$$y_1$$$, $$$x_2$$$, $$$y_2$$$ ($$$1 \le x_1, y_1, x_2, y_{2} \le n$$$, $$$x_1 \neq y_1$$$, $$$x_2 \neq y_2$$$) — this way you remove the edge $$$(x_1, y_1)$$$ and add an undirected edge $$$(x_2, y_2)$$$.

Note that the edge $$$(x_1, y_1)$$$ must be present in the graph at the moment of removing.

Sample Input:

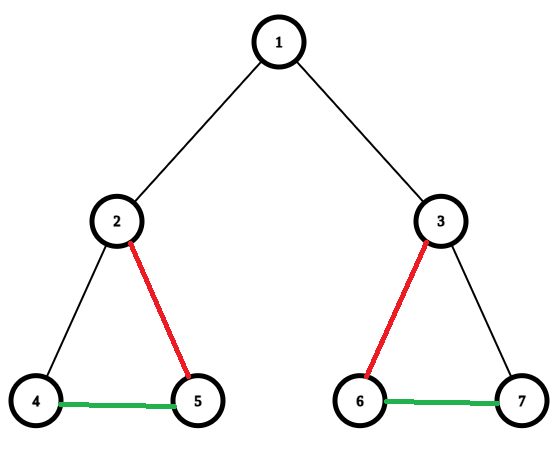
2
7
1 2
1 3
2 4
2 5
3 6
3 7
4
1 2
1 3
3 4

Sample Output:

2
2 5 6 7
3 6 4 5
0

Note:

Note the graph can be unconnected after a certain operation.

Consider the first test case of the example:

The red edges are removed, and the green ones are added.