Preparando MOJI
Let us call a point of the plane admissible if its coordinates are positive integers less than or equal to $$$200$$$.
There is an invisible rectangle such that:
In order to guess it, you may ask at most $$$4$$$ queries.
In each query, you choose a nonempty subset of the admissible points and you are told how many of the chosen points are inside or on the boundary of the invisible rectangle.
To ask a query (of the kind described in the statement), you shall print two lines:
When you have identified the perimeter $$$p$$$ of the invisible rectangle, you must print "! $$$p$$$" (without quotes) and terminate your program.
If you ask more than $$$4$$$ queries or if one of the queries is malformed, the interactor terminates immediately and your program receives verdict Wrong Answer.
The interactor may be adaptive (i.e., the hidden rectangle may not be chosen before the beginning of the interaction).
After printing a query do not forget to output end of line and flush the output. Otherwise, you will get Idleness limit exceeded. To do this, use:
Hacks
To hack a solution, use the following format.
The input has only one line, containing the $$$4$$$ integers $$$x_0$$$, $$$y_0$$$, $$$x_1$$$, $$$y_1$$$ ($$$1\le x_0<x_1\le 200$$$, $$$1\le y_0 < y_1 \le 200$$$) — $$$(x_0,y_0)$$$ is the bottom-left vertex of the hidden rectangle and $$$(x_1, y_1)$$$ is the top-right vertex of the hidden rectangle.
Note that for hacks the interaction won't be adaptive.
13 5 123 80
2 2 4 4
1 1 200 200
The following is an example of interaction for the first sample intended to show the format of the queries. $$$$$$ \begin{array}{l|l|l} \text{Query (contestant program)} & \text{Answer (interactor)} & \text{Explanation} \\ \hline \mathtt{?\ 4} & & \text{We choose the $4$ vertices of} \\ \mathtt{13\ 5\ 13\ 80\ 123\ 5\ 123\ 80} & \mathtt{4} &\text{the hidden rectangle.}\\ \hline \mathtt{?\ 5} & & \text{We choose $4$ points just outside the hidden}\\ \mathtt{100\ 4\ 100\ 81\ 12\ 40\ 124\ 40\ 50\ 50} & \mathtt{1}& \text{rectangle and also the point $(50,50)$.}\\ \hline \mathtt{?\ 2} & & \text{We choose the points $(1, 1)$} \\ \mathtt{200\ 200\ 1\ 1} & \mathtt{0} & \text{and $(200,200)$.}\\ \hline \mathtt{!\ 370} & & \text{This is the correct perimeter.} \end{array} $$$$$$
For the second sample, a possible interaction is the following. $$$$$$ \begin{array}{l|l|l} \text{Query (contestant program)} & \text{Answer (interactor)} & \text{Explanation} \\ \hline \mathtt{?\ 4} & & \text{We choose the points $(3, 2)$, $(4, 1)$,} \\ \mathtt{3\ 2\ 4\ 1\ 5\ 2\ 4\ 3} & 2 & \text{$(5, 2)$ and $(4, 3)$.} \\ \hline \mathtt{?\ 7} & & \text{We choose the points $(1, 4)$, $(2, 4)$,} \\ \mathtt{1\ 4\ 2\ 4\ 1\ 5\ 2\ 5\ 5\ 5\ 5\ 6\ 6\ 5} & 1 & \text{$(1, 5)$, $(2, 5)$, $(5, 5)$, $(5, 6)$ and $(6, 5)$.} \\ \hline \mathtt{!\ 8} & & \text{This is the correct perimeter.} \end{array} $$$$$$ The situation is shown in the following picture:
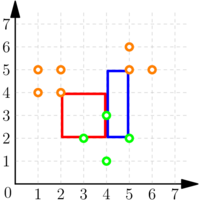
The green points are the ones belonging to the first query, while the orange points are the ones belonging to the second query. One can see that there are exactly two rectangles consistent with the interactor's answers: