You

5000ms

262144K

Description:

You are given a tree with $$$n$$$ nodes. As a reminder, a tree is a connected undirected graph without cycles.

Let $$$a_1, a_2, \ldots, a_n$$$ be a sequence of integers. Perform the following operation exactly $$$n$$$ times:

Select an unerased node $$$u$$$. Assign $$$a_u :=$$$ number of unerased nodes adjacent to $$$u$$$. Then, erase the node $$$u$$$ along with all edges that have it as an endpoint.

For each integer $$$k$$$ from $$$1$$$ to $$$n$$$, find the number, modulo $$$998\,244\,353$$$, of different sequences $$$a_1, a_2, \ldots, a_n$$$ that satisfy the following conditions:

it is possible to obtain $$$a$$$ by performing the aforementioned operations exactly $$$n$$$ times in some order.
$$$\operatorname{gcd}(a_1, a_2, \ldots, a_n) = k$$$. Here, $$$\operatorname{gcd}$$$ means the greatest common divisor of the elements in $$$a$$$.

Input:

The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10\,000$$$) — the number of test cases.

The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 10^5$$$).

Each of the next $$$n - 1$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n$$$) indicating there is an edge between vertices $$$u$$$ and $$$v$$$. It is guaranteed that the given edges form a tree.

It is guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$3 \cdot 10^5$$$.

Output:

For each test case, print $$$n$$$ integers in a single line, where for each $$$k$$$ from $$$1$$$ to $$$n$$$, the $$$k$$$-th integer denotes the answer when $$$\operatorname{gcd}$$$ equals to $$$k$$$.

Sample Input:

Sample Output:

3 1 0
2 0

Note:

In the first test case,

$\text{[math]}$

If we delete the nodes in order $$$1 \rightarrow 2 \rightarrow 3$$$ or $$$1 \rightarrow 3 \rightarrow 2$$$, then the obtained sequence will be $$$a = [2, 0, 0]$$$ which has $$$\operatorname{gcd}$$$ equals to $$$2$$$.
If we delete the nodes in order $$$2 \rightarrow 1 \rightarrow 3$$$, then the obtained sequence will be $$$a = [1, 1, 0]$$$ which has $$$\operatorname{gcd}$$$ equals to $$$1$$$.
If we delete the nodes in order $$$3 \rightarrow 1 \rightarrow 2$$$, then the obtained sequence will be $$$a = [1, 0, 1]$$$ which has $$$\operatorname{gcd}$$$ equals to $$$1$$$.
If we delete the nodes in order $$$2 \rightarrow 3 \rightarrow 1$$$ or $$$3 \rightarrow 2 \rightarrow 1$$$, then the obtained sequence will be $$$a = [0, 1, 1]$$$ which has $$$\operatorname{gcd}$$$ equals to $$$1$$$.

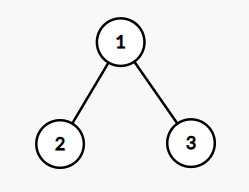
Note that here we are counting the number of different sequences, not the number of different orders of deleting nodes.

Informação

Provedor Codeforces

Código CF1554E