Preparando MOJI
This is the easy version of the problem. The only difference between the two versions is the constraint on $$$n$$$. You can make hacks only if all versions of the problem are solved.
A forest is an undirected graph without cycles (not necessarily connected).
Mocha and Diana are friends in Zhijiang, both of them have a forest with nodes numbered from $$$1$$$ to $$$n$$$, and they would like to add edges to their forests such that:
Mocha and Diana want to know the maximum number of edges they can add, and which edges to add.
The first line contains three integers $$$n$$$, $$$m_1$$$ and $$$m_2$$$ ($$$1 \le n \le 1000$$$, $$$0 \le m_1, m_2 < n$$$) — the number of nodes and the number of initial edges in Mocha's forest and Diana's forest.
Each of the next $$$m_1$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \neq v$$$) — the edges in Mocha's forest.
Each of the next $$$m_2$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \neq v$$$) — the edges in Diana's forest.
The first line contains only one integer $$$h$$$, the maximum number of edges Mocha and Diana can add (in each forest).
Each of the next $$$h$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \neq v$$$) — the edge you add each time.
If there are multiple correct answers, you can print any one of them.
3 2 2 1 2 2 3 1 2 1 3
0
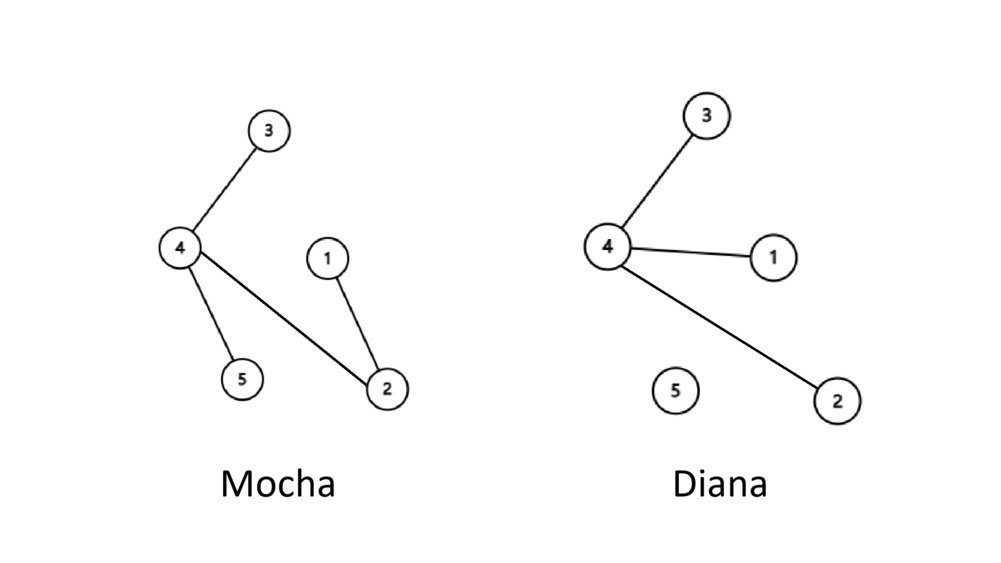
5 3 2 5 4 2 1 4 3 4 3 1 4
1 2 4
8 1 2 1 7 2 6 1 5
5 5 2 2 3 3 4 4 7 6 8
In the first example, we cannot add any edge.
In the second example, the initial forests are as follows.
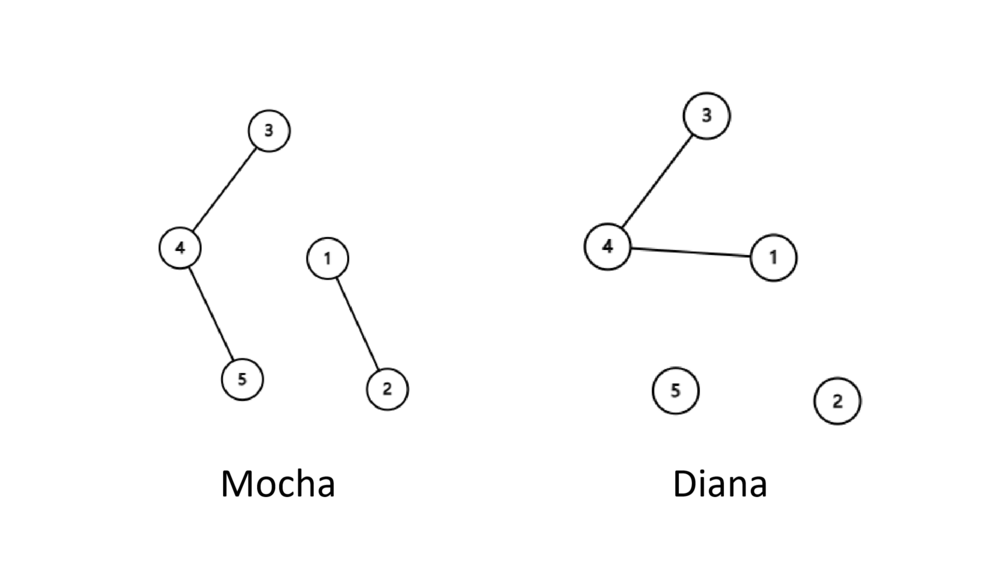
We can add an edge $$$(2, 4)$$$.