Infinity Table

Polycarp has found a table having an infinite number of rows and columns. The rows are numbered from $$$1$$$, starting from the topmost one. The columns are numbered from $$$1$$$, starting from the leftmost one.

Initially, the table hasn't been filled and Polycarp wants to fix it. He writes integers from $$$1$$$ and so on to the table as follows.

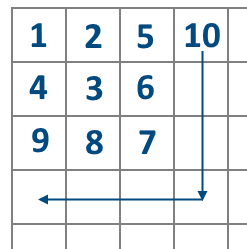The figure shows the placement of the numbers from $$$1$$$ to $$$10$$$. The following actions are denoted by the arrows.

The leftmost topmost cell of the table is filled with the number $$$1$$$. Then he writes in the table all positive integers beginning from $$$2$$$ sequentially using the following algorithm.

First, Polycarp selects the leftmost non-filled cell in the first row and fills it. Then, while the left neighbor of the last filled cell is filled, he goes down and fills the next cell. So he goes down until the last filled cell has a non-filled neighbor to the left (look at the vertical arrow going down in the figure above).

After that, he fills the cells from the right to the left until he stops at the first column (look at the horizontal row in the figure above). Then Polycarp selects the leftmost non-filled cell in the first row, goes down, and so on.

A friend of Polycarp has a favorite number $$$k$$$. He wants to know which cell will contain the number. Help him to find the indices of the row and the column, such that the intersection of the row and the column is the cell containing the number $$$k$$$.