Polygon

Description:

Input:

The first line contains two integers $$$n$$$, $$$k$$$ ($$$3 \le n \le 200$$$, $$$0 \le k \le n-3$$$).

The following $$$n$$$ lines describe vertices of the polygon in anticlockwise direction. The $$$i$$$-th line contains two integers $$$x_i$$$, $$$y_i$$$ ($$$|x_i|, |y_i| \le 10^8$$$) — the coordinates of the $$$i$$$-th vertex.

It is guaranteed that the polygon is convex and that no two adjacent sides are parallel.

Output:

Print one integer: the maximum possible area of the smallest region after making $$$k$$$ cuts multiplied by $$$2$$$.

Sample Input:

8 4
-2 -4
2 -2
4 2
1 5
0 5
-4 4
-5 0
-5 -1

Sample Output:

11

Sample Input:

6 3
2 -2
2 -1
1 2
0 2
-2 1
-1 0

Sample Output:

3

Note:

In the first example, it's optimal to make cuts between the following pairs of vertices:

• $$$(-2, -4)$$$ and $$$(4, 2)$$$,
• $$$(-2, -4)$$$ and $$$(1, 5)$$$,
• $$$(-5, -1)$$$ and $$$(1, 5)$$$,
• $$$(-5, 0)$$$ and $$$(0, 5)$$$.

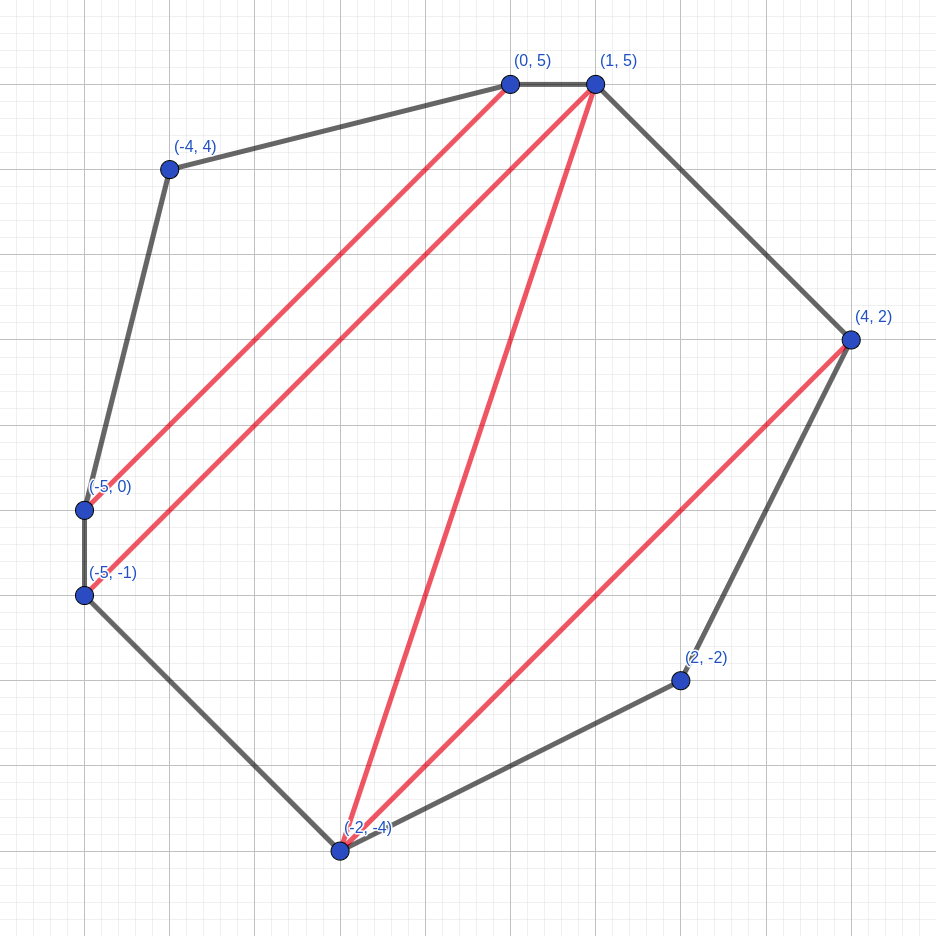Points $$$(-5, -1)$$$, $$$(1, 5)$$$, $$$(0, 5)$$$, $$$(-5, 0)$$$ determine the smallest region with double area of $$$11$$$.

In the second example, it's optimal to make cuts between the following pairs of vertices:

• $$$(2, -1)$$$ and $$$(0, 2)$$$,
• $$$(2, -1)$$$ and $$$(1, 0)$$$,
• $$$(-1, 0)$$$ and $$$(0, 2)$$$.

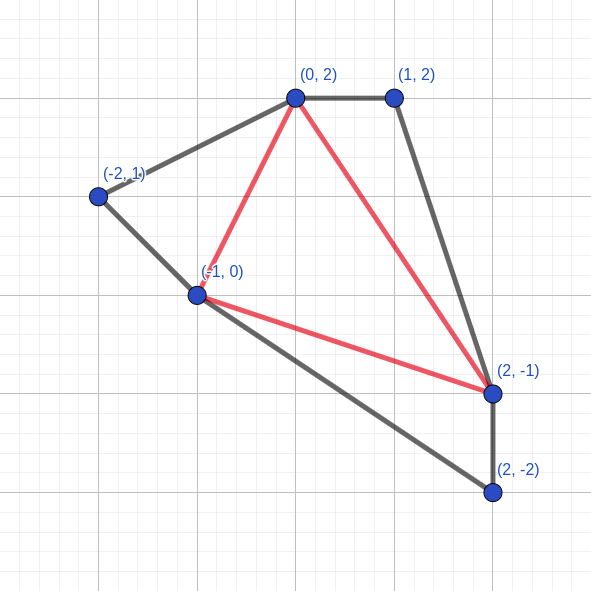Points $$$(2, -2)$$$, $$$(2, -1)$$$, $$$(-1, 0)$$$ determine one of the smallest regions with double area of $$$3$$$.