Illusions of the Desert

3000ms

524288K

Description:

Chanek Jones is back, helping his long-lost relative Indiana Jones, to find a secret treasure in a maze buried below a desert full of illusions.

The map of the labyrinth forms a tree with $$$n$$$ rooms numbered from $$$1$$$ to $$$n$$$ and $$$n - 1$$$ tunnels connecting them such that it is possible to travel between each pair of rooms through several tunnels.

To prevent grave robbers, the maze can change the illusion rate of any room in it. Chanek and Indiana would ask $$$q$$$ queries.

There are two types of queries to be done:

$$$1\ u\ c$$$ — The illusion rate of the $$$x$$$-th room is changed to $$$c$$$ ($$$1 \leq u \leq n$$$, $$$0 \leq |c| \leq 10^9$$$).
$$$2\ u\ v$$$ — Chanek and Indiana ask you the minimum sum of energy needed to take the secret treasure at room $$$v$$$ if they are initially at room $$$u$$$ ($$$1 \leq u, v \leq n$$$).

Help them, so you can get a portion of the treasure!

Input:

The first line contains two integers $$$n$$$ and $$$q$$$ ($$$2 \leq n \leq 10^5$$$, $$$1 \leq q \leq 10^5$$$) — the number of rooms in the maze and the number of queries.

The second line contains $$$n$$$ integers $$$a_1, a_2, \ldots, a_n$$$ ($$$0 \leq |a_i| \leq 10^9$$$) — inital illusion rate of each room.

The $$$i$$$-th of the next $$$n-1$$$ lines contains two integers $$$s_i$$$ and $$$t_i$$$ ($$$1 \leq s_i, t_i \leq n$$$), meaning there is a tunnel connecting $$$s_i$$$-th room and $$$t_i$$$-th room. The given edges form a tree.

The next $$$q$$$ lines contain the query as described. The given queries are valid.

Output:

For each type $$$2$$$ query, output a line containing an integer — the minimum sum of energy needed for Chanek and Indiana to take the secret treasure.

Sample Input:

6 4
10 -9 2 -1 4 -6
1 5
5 4
5 6
6 2
6 3
2 1 2
1 1 -3
2 1 2
2 3 3

Sample Output:

39
32
0

Note:

$\text{[math]}$

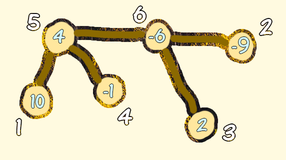
In the first query, their movement from the $$$1$$$-st to the $$$2$$$-nd room is as follows.

$$$1 \rightarrow 5$$$ — takes $$$\max(|10 + 4|, |10 - 4|) = 14$$$ energy.
$$$5 \rightarrow 6$$$ — takes $$$\max(|4 + (-6)|, |4 - (-6)|) = 10$$$ energy.
$$$6 \rightarrow 2$$$ — takes $$$\max(|-6 + (-9)|, |-6 - (-9)|) = 15$$$ energy.

In total, it takes $$$39$$$ energy.

In the second query, the illusion rate of the $$$1$$$-st room changes from $$$10$$$ to $$$-3$$$.

In the third query, their movement from the $$$1$$$-st to the $$$2$$$-nd room is as follows.

$$$1 \rightarrow 5$$$ — takes $$$\max(|-3 + 4|, |-3 - 4|) = 7$$$ energy.
$$$5 \rightarrow 6$$$ — takes $$$\max(|4 + (-6)|, |4 - (-6)|) = 10$$$ energy.
$$$6 \rightarrow 2$$$ — takes $$$\max(|-6 + (-9)|, |-6 - (-9)|) = 15$$$ energy.

Now, it takes $$$32$$$ energy.

Informação

Provedor Codeforces

Código CF1575I