Preparando MOJI
Mr. Chanek wants to knit a batik, a traditional cloth from Indonesia. The cloth forms a grid $$$a$$$ with size $$$n \times m$$$. There are $$$k$$$ colors, and each cell in the grid can be one of the $$$k$$$ colors.
Define a sub-rectangle as an ordered pair of two cells $$$((x_1, y_1), (x_2, y_2))$$$, denoting the top-left cell and bottom-right cell (inclusively) of a sub-rectangle in $$$a$$$. Two sub-rectangles $$$((x_1, y_1), (x_2, y_2))$$$ and $$$((x_3, y_3), (x_4, y_4))$$$ have the same pattern if and only if the following holds:
Count the number of possible batik color combinations, such that the subrectangles $$$((a_x, a_y),(a_x + r - 1, a_y + c - 1))$$$ and $$$((b_x, b_y),(b_x + r - 1, b_y + c - 1))$$$ have the same pattern.
Output the answer modulo $$$10^9 + 7$$$.
The first line contains five integers $$$n$$$, $$$m$$$, $$$k$$$, $$$r$$$, and $$$c$$$ ($$$1 \leq n, m \leq 10^9$$$, $$$1 \leq k \leq 10^9$$$, $$$1 \leq r \leq \min(10^6, n)$$$, $$$1 \leq c \leq \min(10^6, m)$$$) — the size of the batik, the number of colors, and size of the sub-rectangle.
The second line contains four integers $$$a_x$$$, $$$a_y$$$, $$$b_x$$$, and $$$b_y$$$ ($$$1 \leq a_x, b_x \leq n$$$, $$$1 \leq a_y, b_y \leq m$$$) — the top-left corners of the first and second sub-rectangle. Both of the sub-rectangles given are inside the grid ($$$1 \leq a_x + r - 1$$$, $$$b_x + r - 1 \leq n$$$, $$$1 \leq a_y + c - 1$$$, $$$b_y + c - 1 \leq m$$$).
Output an integer denoting the number of possible batik color combinations modulo $$$10^9 + 7$$$.
3 3 2 2 2 1 1 2 2
32
4 5 170845 2 2 1 4 3 1
756680455
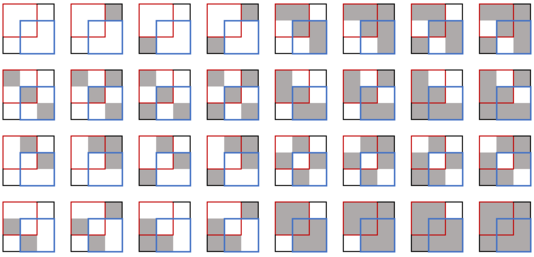
The following are all $$$32$$$ possible color combinations in the first example.