Dragon Curve

A dragon curve is a self-similar fractal curve. In this problem, it is a curve that consists of straight-line segments of the same length connected at right angles. A simple way to construct a dragon curve is as follows: take a strip of paper, fold it in half $$$n$$$ times in the same direction, then partially unfold it such that the segments are joined at right angles. This is illustrated here:

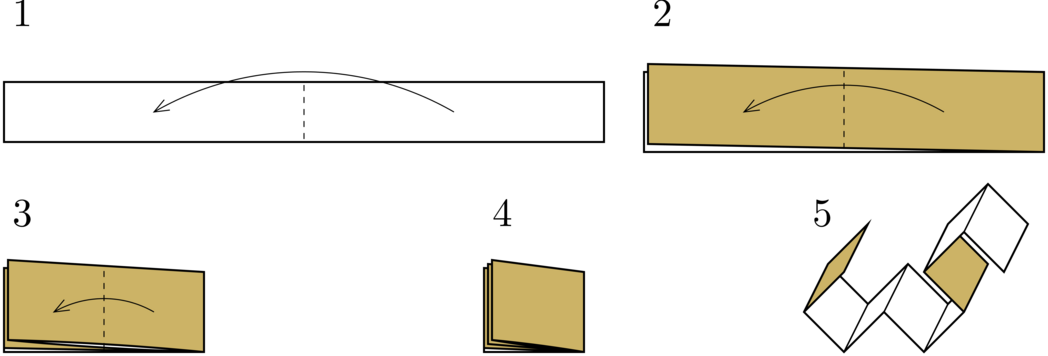
In this example, a dragon curve of order $$$3$$$ is constructed. In general, a dragon curve of a higher order will have a dragon curve of a lower order as its prefix. This allows us to define a dragon curve of infinite order, which is the limit of dragon curves of a finite order as the order approaches infinity.

Consider four dragon curves of infinite order. Each starts at the origin (the point $$$(0,0)$$$), and the length of each segment is $$$\sqrt2$$$. The first segments of the curves end at the points $$$(1,1)$$$, $$$(-1,1)$$$, $$$(-1,-1)$$$ and $$$(1,-1)$$$, respectively. The first turn of each curve is left (that is, the second segment of the first curve ends at the point $$$(0,2)$$$). In this case, every segment is a diagonal of an axis-aligned unit square with integer coordinates, and it can be proven that there is exactly one segment passing through every such square.

Given a point $$$(x,y)$$$, your task is to find on which of the four curves lies the segment passing through the square with the opposite corners at $$$(x,y)$$$ and $$$(x+1,y+1)$$$, as well as the position of that segment on that curve. The curves are numbered $$$1$$$ through $$$4$$$. Curve $$$1$$$ goes through $$$(1,1)$$$, $$$2$$$ through $$$(-1,1)$$$, $$$3$$$ through $$$(-1,-1)$$$, and $$$4$$$ through $$$(1,-1)$$$. The segments are numbered starting with $$$1$$$.