Description:
You are given an array of integers $$$a$$$ of size $$$n$$$ and a permutation $$$p$$$ of size $$$n$$$. There are $$$q$$$ queries of three types coming to you:
- For given numbers $$$l$$$ and $$$r$$$, calculate the sum in array $$$a$$$ on the segment from $$$l$$$ to $$$r$$$: $$$\sum\limits_{i=l}^{r} a_i$$$.
- You are given two numbers $$$v$$$ and $$$x$$$. Let's build a directed graph from the permutation $$$p$$$: it has $$$n$$$ vertices and $$$n$$$ edges $$$i \to p_i$$$. Let $$$C$$$ be the set of vertices that are reachable from $$$v$$$ in this graph. You should add $$$x$$$ to all $$$a_u$$$ such that $$$u$$$ is in $$$C$$$.
- You are given indices $$$i$$$ and $$$j$$$. You should swap $$$p_i$$$ and $$$p_j$$$.
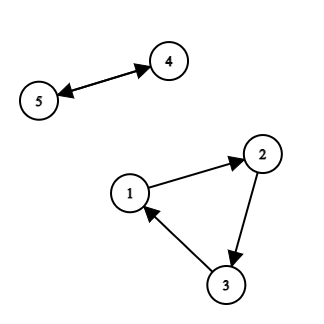 The graph corresponding to the permutation $$$[2, 3, 1, 5, 4]$$$.
The graph corresponding to the permutation $$$[2, 3, 1, 5, 4]$$$. Please, process all queries and print answers to queries of type $$$1$$$.
Input:
The first line contains a single integer $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — the size of the array and permutation.
The second line contains $$$n$$$ integers $$$a_1, a_2, \ldots, a_n$$$ ($$$-10^8 \le a_i \le 10^8$$$).
The third line contains $$$n$$$ distinct integers $$$p_1, p_2, \ldots, p_n$$$ ($$$1 \le p_i \le n$$$).
The fourth line contains a single integer $$$q$$$ — the number of queries ($$$1 \le q \le 2 \cdot 10^5$$$).
Next $$$q$$$ lines contain description of queries. The $$$i$$$-th of them starts with an integer $$$t_i$$$ ($$$1 \le t_i \le 3$$$) — the query type.
- If $$$t_i = 1$$$, then the $$$i$$$-th line also contains two integers $$$l$$$, $$$r$$$ ($$$1 \le l \le r \le n$$$).
- If $$$t_i = 2$$$, then the $$$i$$$-th line also contains two integers $$$v$$$, $$$x$$$ ($$$1 \le v \le n$$$, $$$-10^8 \le x \le 10^8$$$).
- If $$$t_i = 3$$$, then the $$$i$$$-th line also contains also two integers $$$i$$$, $$$j$$$ ($$$1 \le i, j \le n$$$).
Output:
For every first type query, print a single integer — the answer to this query.
Sample Input:
5
6 9 -5 3 0
2 3 1 5 4
6
1 1 5
2 1 1
1 1 5
3 1 5
2 1 -1
1 1 5
Sample Output:
13
16
11
Sample Input:
8
-15 52 -4 3 5 9 0 5
2 4 6 8 1 3 5 7
10
2 2 2
2 5 -1
1 1 8
1 1 5
1 5 8
3 1 6
2 1 50
1 1 8
2 6 -20
1 1 8
Sample Output:
61
45
22
461
301
Sample Input:
1
1
1
1
1 1 1
Sample Output:
1
Note:
In the first example:
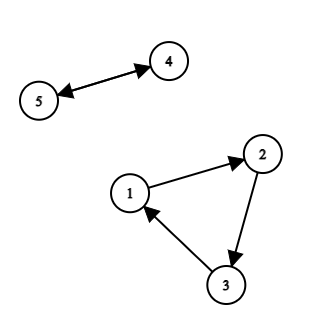 The graph corresponding to the initial permutation.
The graph corresponding to the initial permutation. There are $$$6$$$ queries.
- The sum on the segment from $$$1$$$ to $$$5$$$ is $$$a_1 + a_2 + a_3 + a_4 + a_5 = 6 + 9 + (-5) + 3 + 0 = 13$$$.
- If we start from $$$1$$$, we can reach $$$\{1, 2, 3\}$$$. After this query $$$a$$$ is: $$$[7, 10, -4, 3, 0]$$$.
- The sum on the segment from $$$1$$$ to $$$5$$$ is $$$a_1 + a_2 + a_3 + a_4 + a_5 = 6 + 9 + (-5) + 3 + 0 = 16$$$.
- After this query $$$p = [4, 3, 1, 5, 2]$$$.
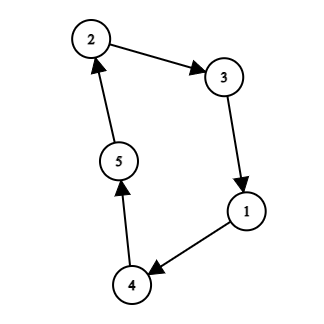 The graph corresponding to the new permutation.
The graph corresponding to the new permutation. - If we start from $$$2$$$, we can reach $$$\{1, 2, 3, 4, 5\}$$$. After this query $$$a$$$ is: $$$[6, 9, -5, 2, -1]$$$.
- The sum on the segment from $$$1$$$ to $$$5$$$ is $$$a_1 + a_2 + a_3 + a_4 + a_5 = 6 + 9 + (-5) + 2 + (-1) = 11$$$.
 The graph corresponding to the permutation $$$[2, 3, 1, 5, 4]$$$.
The graph corresponding to the permutation $$$[2, 3, 1, 5, 4]$$$.  The graph corresponding to the initial permutation.
The graph corresponding to the initial permutation.  The graph corresponding to the new permutation.
The graph corresponding to the new permutation.