Staircases

2000ms

262144K

Description:

You are given a matrix, consisting of $$$n$$$ rows and $$$m$$$ columns. The rows are numbered top to bottom, the columns are numbered left to right.

Each cell of the matrix can be either free or locked.

Let's call a path in the matrix a staircase if it:

starts and ends in the free cell;
visits only free cells;
has one of the two following structures:
1. the second cell is $$$1$$$ to the right from the first one, the third cell is $$$1$$$ to the bottom from the second one, the fourth cell is $$$1$$$ to the right from the third one, and so on;
2. the second cell is $$$1$$$ to the bottom from the first one, the third cell is $$$1$$$ to the right from the second one, the fourth cell is $$$1$$$ to the bottom from the third one, and so on.

In particular, a path, consisting of a single cell, is considered to be a staircase.

Here are some examples of staircases:

$\text{[math]}$

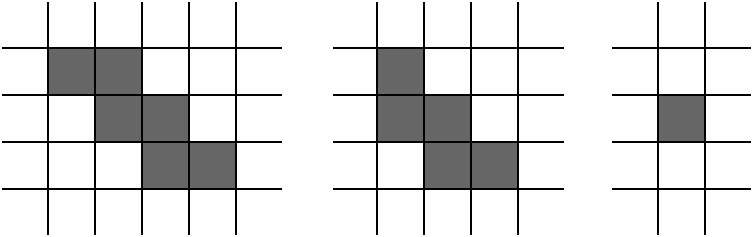
Initially all the cells of the matrix are free.

You have to process $$$q$$$ queries, each of them flips the state of a single cell. So, if a cell is currently free, it makes it locked, and if a cell is currently locked, it makes it free.

Print the number of different staircases after each query. Two staircases are considered different if there exists such a cell that appears in one path and doesn't appear in the other path.

Input:

The first line contains three integers $$$n$$$, $$$m$$$ and $$$q$$$ ($$$1 \le n, m \le 1000$$$; $$$1 \le q \le 10^4$$$) — the sizes of the matrix and the number of queries.

Each of the next $$$q$$$ lines contains two integers $$$x$$$ and $$$y$$$ ($$$1 \le x \le n$$$; $$$1 \le y \le m$$$) — the description of each query.

Output:

Print $$$q$$$ integers — the $$$i$$$-th value should be equal to the number of different staircases after $$$i$$$ queries. Two staircases are considered different if there exists such a cell that appears in one path and doesn't appear in the other path.

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Sample Input:

1000 1000 2
239 634
239 634

Sample Output:

1332632508
1333333000

Informação

Provedor Codeforces

Código CF1598E