Treelabeling

2000ms

262144K

Description:

Eikooc and Sushi play a game.

The game is played on a tree having $$$n$$$ nodes numbered $$$1$$$ to $$$n$$$. Recall that a tree having $$$n$$$ nodes is an undirected, connected graph with $$$n-1$$$ edges.

They take turns alternately moving a token on the tree. Eikooc makes the first move, placing the token on any node of her choice. Sushi makes the next move, followed by Eikooc, followed by Sushi, and so on. In each turn after the first, a player must move the token to a node $$$u$$$ such that

$$$u$$$ is adjacent to the node $$$v$$$ the token is currently on
$$$u$$$ has not been visited before
$$$u \oplus v \leq min(u, v)$$$

Here $$$x \oplus y$$$ denotes the bitwise XOR operation on integers $$$x$$$ and $$$y$$$.

Both the players play optimally. The player who is unable to make a move loses.

The following are examples which demonstrate the rules of the game.

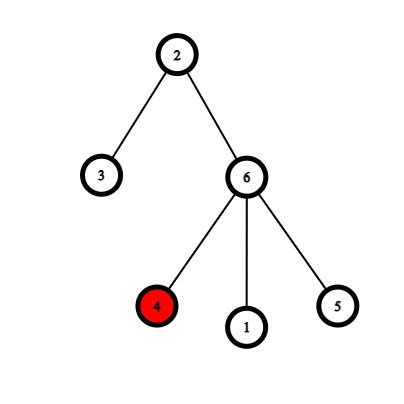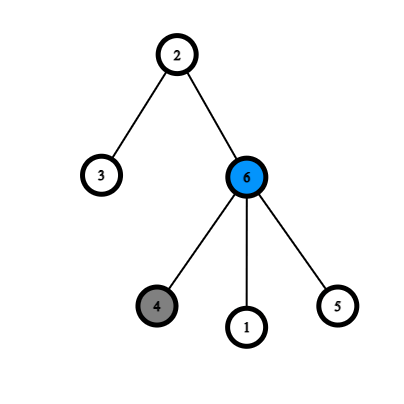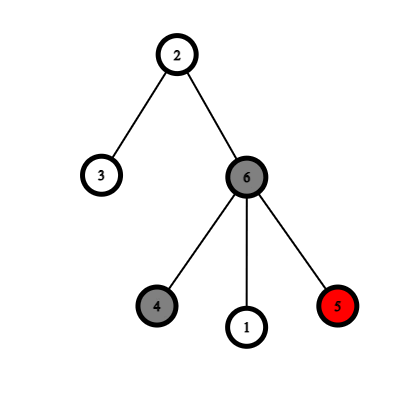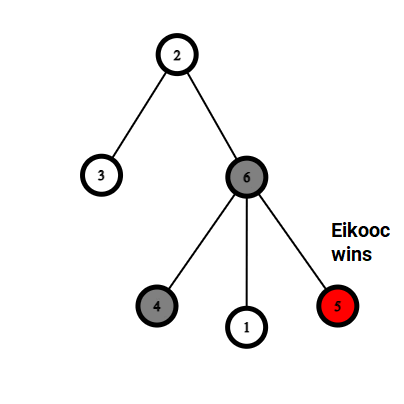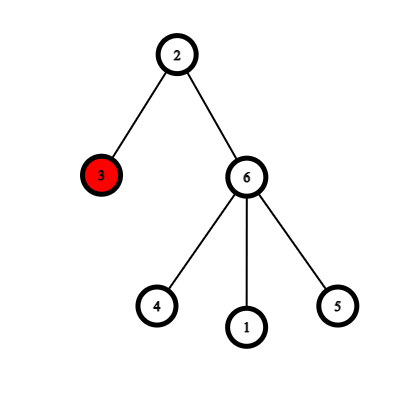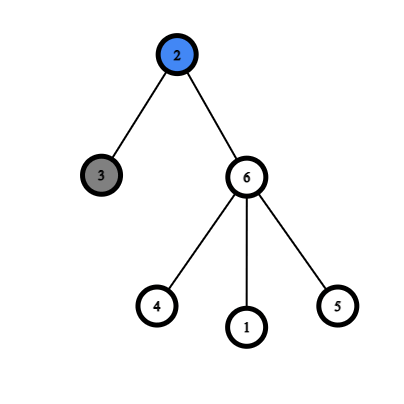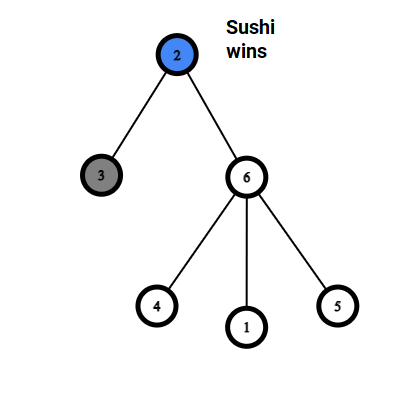$\text{[math]}$ Suppose Eikooc starts the game by placing the token at node $$$4$$$. Sushi then moves the token to node $$$6$$$, which is unvisited and adjacent to $$$4$$$. It also holds that $$$6 \oplus 4 = 2 \leq min(6, 4)$$$. In the next turn, Eikooc moves the token to node $$$5$$$, which is unvisited and adjacent to $$$6$$$. It holds that $$$5 \oplus 6 = 3 \leq min(5, 6)$$$. Sushi has no more moves to play, so she loses.

$\text{[math]}$ Suppose Eikooc starts the game by placing the token at node $$$3$$$. Sushi moves the token to node $$$2$$$, which is unvisited and adjacent to $$$3$$$. It also holds that $$$3 \oplus 2 = 1 \leq min(3, 2)$$$. Eikooc cannot move the token to node $$$6$$$ since $$$6 \oplus 2 = 4 \nleq min(6, 2)$$$. Since Eikooc has no moves to play, she loses.

Before the game begins, Eikooc decides to sneakily relabel the nodes of the tree in her favour. Formally, a relabeling is a permutation $$$p$$$ of length $$$n$$$ (sequence of $$$n$$$ integers wherein each integer from $$$1$$$ to $$$n$$$ occurs exactly once) where $$$p_i$$$ denotes the new numbering of node $$$i$$$.

She wants to maximize the number of nodes she can choose in the first turn which will guarantee her a win. Help Eikooc find any relabeling which will help her do so.

Input:

The first line contains a single integer $$$t~(1 \le t \le 10^5)$$$ — the number of test cases. The description of each test case is as follows.

The first line of each test case contains an integer $$$n~(1 \le n \le 2 \cdot 10^5)$$$ — the number of nodes in the tree.

The next $$$n-1$$$ lines contain two integers $$$u$$$ and $$$v$$$ $$$(1 \le u, v \le n; u \neq v)$$$ — denoting an edge between nodes $$$u$$$ and $$$v$$$.

It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.

Output:

For each test case print any suitable relabeling — a permutation of length $$$n$$$ which maximizes the number of nodes that can be chosen in the first turn that guarantee a win for Eikooc. If there are multiple such relabelings, you may print any of them.

Sample Input:

Sample Output:

1
2 1
1 2 3

Note:

In the first test case, Eikooc has only one choice. Sushi will have no moves to play after Eikooc chooses this node and Eikooc will win.

In the second test case, $$$1 \oplus 2 = 3 \nleq min(1, 2)$$$. Hence, after Eikooc picks either of the nodes, Sushi will have no moves to play and Eikooc will win. Both $$$\{1, 2\}$$$ and $$$\{2, 1\}$$$ are optimal relabelings.

Informação

Provedor Codeforces

Código CF1605D