Tree Queries

Description:

Input:

The first line contains one integer $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — the number of vertices in the tree.

Then $$$n-1$$$ lines follow, the $$$i$$$-th of them contains two integers $$$x_i$$$ and $$$y_i$$$ ($$$1 \le x_i, y_i \le n$$$; $$$x_i \ne y_i$$$) — the endpoints of the $$$i$$$-th edge. These edges form a tree.

The next line contains one integer $$$q$$$ ($$$1 \le q \le 2 \cdot 10^5$$$) — the number of queries.

Then $$$q$$$ lines follow, the $$$j$$$-th of them contains two integers $$$v_j$$$ and $$$k_j$$$ ($$$1 \le v_j \le n$$$; $$$0 \le k_j \le 2 \cdot 10^5$$$) — the parameters of the $$$j$$$-th query.

Output:

For each query, print one integer — the maximum value of $$$c(v) - m \cdot k$$$ you can achieve.

Sample Input:

8
6 7
3 2
8 3
5 7
7 4
7 1
7 3
6
1 0
1 2
1 3
7 1
5 0
7 200000

Sample Output:

5
2
1
4
0
4

Note:

The tree in the first example is shown in the following picture:

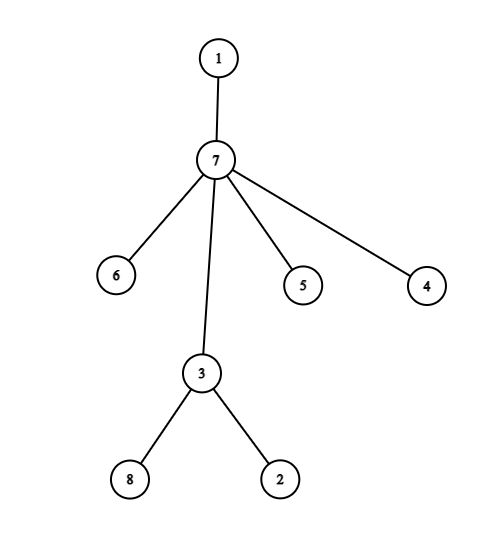
Answers to the queries are obtained as follows:

1. $$$v=1,k=0$$$: you can delete vertices $$$7$$$ and $$$3$$$, so the vertex $$$1$$$ has $$$5$$$ children (vertices $$$2$$$, $$$4$$$, $$$5$$$, $$$6$$$, and $$$8$$$), and the score is $$$5 - 2 \cdot 0 = 5$$$;
2. $$$v=1,k=2$$$: you can delete the vertex $$$7$$$, so the vertex $$$1$$$ has $$$4$$$ children (vertices $$$3$$$, $$$4$$$, $$$5$$$, and $$$6$$$), and the score is $$$4 - 1 \cdot 2 = 2$$$.
3. $$$v=1,k=3$$$: you shouldn't delete any vertices, so the vertex $$$1$$$ has only one child (vertex $$$7$$$), and the score is $$$1 - 0 \cdot 3 = 1$$$;
4. $$$v=7,k=1$$$: you can delete the vertex $$$3$$$, so the vertex $$$7$$$ has $$$5$$$ children (vertices $$$2$$$, $$$4$$$, $$$5$$$, $$$6$$$, and $$$8$$$), and the score is $$$5 - 1 \cdot 1 = 4$$$;
5. $$$v=5,k=0$$$: no matter what you do, the vertex $$$5$$$ will have no children, so the score is $$$0$$$;
6. $$$v=7,k=200000$$$: you shouldn't delete any vertices, so the vertex $$$7$$$ has $$$4$$$ children (vertices $$$3$$$, $$$4$$$, $$$5$$$, and $$$6$$$), and the score is $$$4 - 0 \cdot 200000 = 4$$$.