Pushing Robots

There're $$$n$$$ robots placed on a number line. Initially, $$$i$$$-th of them occupies unit segment $$$[x_i, x_i + 1]$$$. Each robot has a program, consisting of $$$k$$$ instructions numbered from $$$1$$$ to $$$k$$$. The robot performs instructions in a cycle. Each instruction is described by an integer number. Let's denote the number corresponding to the $$$j$$$-th instruction of the $$$i$$$-th robot as $$$f_{i, j}$$$.

Initial placement of robots corresponds to the moment of time $$$0$$$. During one second from moment of time $$$t$$$ ($$$0 \le t$$$) until $$$t + 1$$$ the following process occurs:

1. Each robot performs $$$(t \bmod k + 1)$$$-th instruction from its list of instructions. Robot number $$$i$$$ takes number $$$F = f_{i, (t \bmod k + 1)}$$$. If this number is negative (less than zero), the robot is trying to move to the left with force $$$|F|$$$. If the number is positive (more than zero), the robot is trying to move to the right with force $$$F$$$. Otherwise, the robot does nothing.
2. Let's imaginary divide robots into groups of consecutive, using the following algorithm:
   • Initially, each robot belongs to its own group.
   • Let's sum up numbers corresponding to the instructions of the robots from one group. Note that we are summing numbers without taking them by absolute value. Denote this sum as $$$S$$$. We say that the whole group moves together, and does it with force $$$S$$$ by the same rules as a single robot. That is if $$$S$$$ is negative, the group is trying to move to the left with force $$$|S|$$$. If $$$S$$$ is positive, the group is trying to move to the right with force $$$S$$$. Otherwise, the group does nothing.
   • If one group is trying to move, and in the direction of movement touches another group, let's unite them. One group is touching another if their outermost robots occupy adjacent unit segments.
   • Continue this process until groups stop uniting.
3. Each robot moves by $$$1$$$ in the direction of movement of its group or stays in place if its group isn't moving. But there's one exception.
4. The exception is if there're two groups of robots, divided by exactly one unit segment, such that the left group is trying to move to the right and the right group is trying to move to the left. Let's denote sum in the left group as $$$S_l$$$ and sum in the right group as $$$S_r$$$. If $$$|S_l| \le |S_r|$$$ only the right group will move. Otherwise, only the left group will move.
5. Note that robots from one group don't glue together. They may separate in the future. The division into groups is imaginary and is needed only to understand how robots will move during one second $$$[t, t + 1]$$$.

An illustration of the process happening during one second:

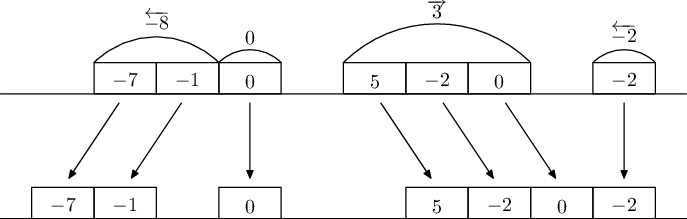
Rectangles represent robots. Numbers inside rectangles correspond to instructions of robots. The final division into groups is marked with arcs. Below are the positions of the robots after moving. Only the left of the two rightmost groups moved. That's because these two groups tried to move towards each other, and were separated by exactly one unit segment.

Look at the examples for a better understanding of the process.

You need to answer several questions. What is the position of $$$a_i$$$-th robot at the moment of time $$$t_i$$$?