Not Quite Lee

1000ms

262144K

Description:

Lee couldn't sleep lately, because he had nightmares. In one of his nightmares (which was about an unbalanced global round), he decided to fight back and propose a problem below (which you should solve) to balance the round, hopefully setting him free from the nightmares.

A non-empty array $$$b_1, b_2, \ldots, b_m$$$ is called good, if there exist $$$m$$$ integer sequences which satisfy the following properties:

The $$$i$$$-th sequence consists of $$$b_i$$$ consecutive integers (for example if $$$b_i = 3$$$ then the $$$i$$$-th sequence can be $$$(-1, 0, 1)$$$ or $$$(-5, -4, -3)$$$ but not $$$(0, -1, 1)$$$ or $$$(1, 2, 3, 4)$$$).
Assuming the sum of integers in the $$$i$$$-th sequence is $$$sum_i$$$, we want $$$sum_1 + sum_2 + \ldots + sum_m$$$ to be equal to $$$0$$$.

You are given an array $$$a_1, a_2, \ldots, a_n$$$. It has $$$2^n - 1$$$ nonempty subsequences. Find how many of them are good.

As this number can be very large, output it modulo $$$10^9 + 7$$$.

An array $$$c$$$ is a subsequence of an array $$$d$$$ if $$$c$$$ can be obtained from $$$d$$$ by deletion of several (possibly, zero or all) elements.

Input:

The first line contains a single integer $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — the size of array $$$a$$$.

The second line contains $$$n$$$ integers $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \le a_i \le 10^9$$$) — elements of the array.

Output:

Print a single integer — the number of nonempty good subsequences of $$$a$$$, modulo $$$10^9 + 7$$$.

Sample Input:

4
2 2 4 7

Sample Output:

Sample Input:

10
12391240 103904 1000000000 4142834 12039 142035823 1032840 49932183 230194823 984293123

Sample Output:

Note:

For the first test, two examples of good subsequences are $$$[2, 7]$$$ and $$$[2, 2, 4, 7]$$$:

For $$$b = [2, 7]$$$ we can use $$$(-3, -4)$$$ as the first sequence and $$$(-2, -1, \ldots, 4)$$$ as the second. Note that subsequence $$$[2, 7]$$$ appears twice in $$$[2, 2, 4, 7]$$$, so we have to count it twice.

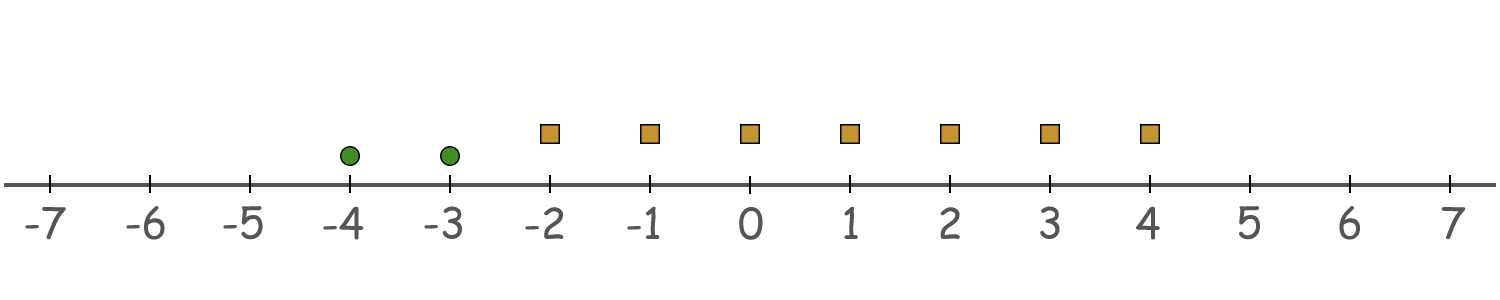$\text{[math]}$ Green circles denote $$$(-3, -4)$$$ and orange squares denote $$$(-2, -1, \ldots, 4)$$$.

For $$$b = [2, 2, 4, 7]$$$ the following sequences would satisfy the properties: $$$(-1, 0)$$$, $$$(-3, -2)$$$, $$$(0, 1, 2, 3)$$$ and $$$(-3, -2, \ldots, 3)$$$

Informação

Provedor Codeforces

Código CF1610D