Unusual Minesweeper

Description:

Input:

The first line of the input contains an integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases in the test.

An empty line is written in front of each test suite.

Next comes a line that contains integers $$$n$$$ and $$$k$$$ ($$$1 \le n \le 2 \cdot 10^5$$$, $$$0 \le k \le 10^9$$$) — the number of mines and the distance that hit by mines during the explosion, respectively.

Then $$$n$$$ lines follow, the $$$i$$$-th of which describes the $$$x$$$ and $$$y$$$ coordinates of the $$$i$$$-th mine and the time until its explosion ($$$-10^9 \le x, y \le 10^9$$$, $$$0 \le timer \le 10^9$$$). It is guaranteed that all mines have different coordinates.

It is guaranteed that the sum of the values $$$n$$$ over all test cases in the test does not exceed $$$2 \cdot 10^5$$$.

Output:

Print $$$t$$$ lines, each of the lines must contain the answer to the corresponding set of input data  — the minimum number of seconds it takes to explode all the mines.

Sample Input:

3

5 0
0 0 1
0 1 4
1 0 2
1 1 3
2 2 9

5 2
0 0 1
0 1 4
1 0 2
1 1 3
2 2 9

6 1
1 -1 3
0 -1 9
0 1 7
-1 0 1
-1 1 9
-1 -1 7

Sample Output:

2
1
0

Note:

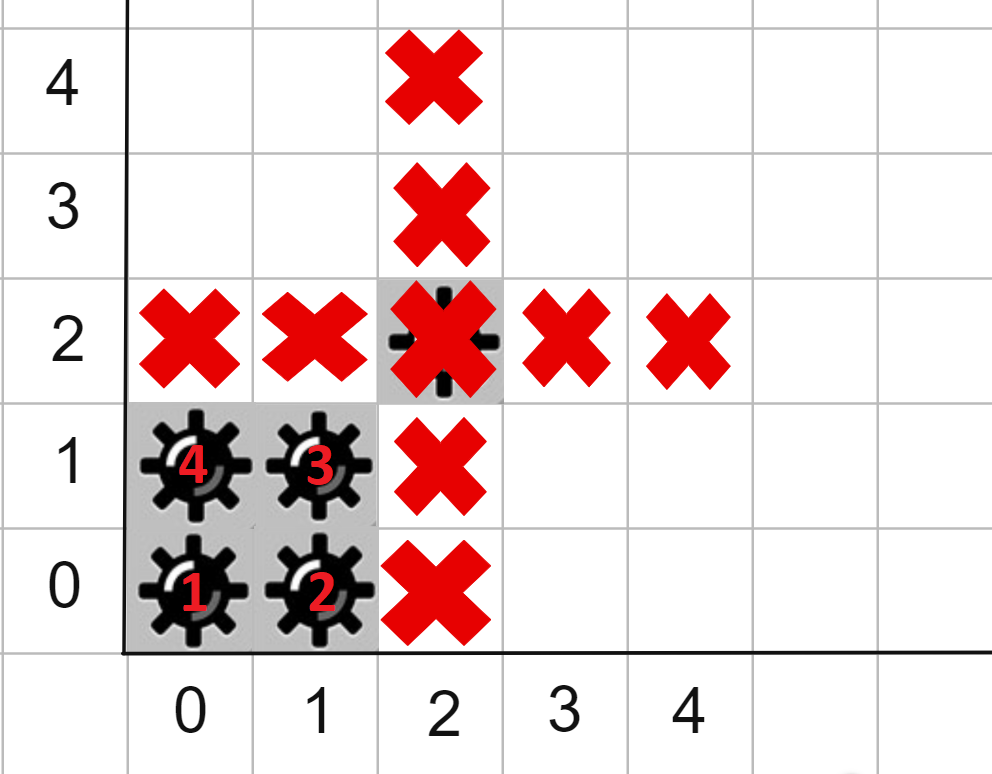
Picture from examples

First example:

• $$$0$$$ second: we explode a mine at the cell $$$(2, 2)$$$, it does not detonate any other mine since $$$k=0$$$.
• $$$1$$$ second: we explode the mine at the cell $$$(0, 1)$$$, and the mine at the cell $$$(0, 0)$$$ explodes itself.
• $$$2$$$ second: we explode the mine at the cell $$$(1, 1)$$$, and the mine at the cell $$$(1, 0)$$$ explodes itself.

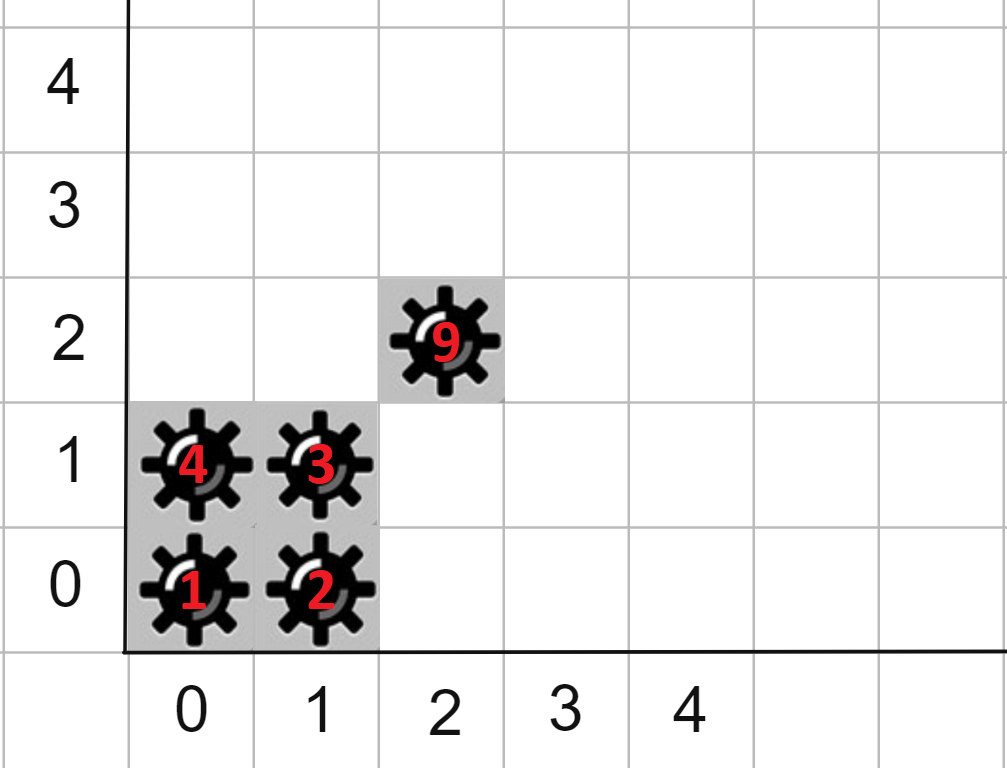
Second example:

• $$$0$$$ second: we explode a mine at the cell $$$(2, 2)$$$ we get:

• $$$1$$$ second: the mine at coordinate $$$(0, 0)$$$ explodes and since $$$k=2$$$ the explosion detonates mines at the cells $$$(0, 1)$$$ and $$$(1, 0)$$$, and their explosions detonate the mine at the cell $$$(1, 1)$$$ and there are no mines left on the field.