MinOr Tree

Description:

Input:

The first line of the input contains an integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases in the input.

An empty line is written in front of each test case.

This is followed by two numbers $$$n$$$ and $$$m$$$ ($$$3 \le n \le 2 \cdot 10^5, n - 1 \le m \le 2 \cdot 10^5$$$) — the number of vertices and edges of the graph, respectively.

The next $$$m$$$ lines contain the description of the edges. Line $$$i$$$ contains three numbers $$$v_i$$$, $$$u_i$$$ and $$$w_i$$$ ($$$1 \le v_i, u_i \le n$$$, $$$1 \le w_i \le 10^9$$$, $$$v_i \neq u_i$$$) — the vertices that the edge connects and its weight.

It is guaranteed that the sum $$$m$$$ and the sum $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$ and each test case contains a connected graph.

Output:

Print $$$t$$$ lines, each of which contains the answer to the corresponding set of input data — the minimum possible spanning tree ority.

Sample Input:

3

3 3
1 2 1
2 3 2
1 3 2

5 7
4 2 7
2 5 8
3 4 2
3 2 1
2 4 2
4 1 2
1 2 2

3 4
1 2 1
2 3 2
1 3 3
3 1 4

Sample Output:

2
10
3

Note:

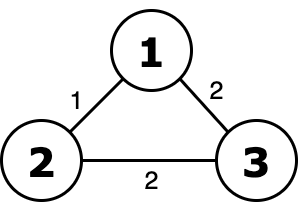Graph from the first test case. 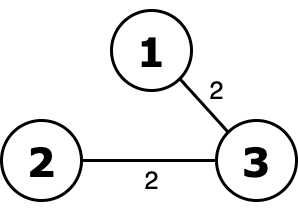Ority of this tree equals to 2 or 2 = 2 and it's minimal. 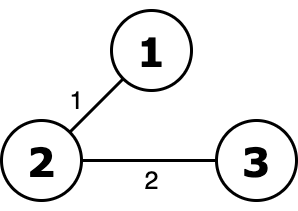Without excluding edge with weight $$$1$$$ ority is 1 or 2 = 3.