Making It Bipartite

Description:

Input:

The input consists of multiple test cases. The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases. Description of the test cases follows.

The first line of each test case contains a single integer $$$n$$$ ($$$1 \le n \le 5\cdot10^4$$$) — the number of vertices in the graph.

The second line of each test case contains $$$n$$$ integers, the $$$i$$$-th of them is the value $$$a_i$$$ ($$$1 \le a_i \le 5\cdot10^4$$$) assigned to the $$$i$$$-th vertex, all values $$$a_i$$$ are different.

It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$5\cdot10^4$$$.

Output:

For each test case print a single integer — the minimum number of vertices to remove such that the remaining graph is bipartite.

Sample Input:

4
4
8 4 2 1
4
30 2 3 5
5
12 4 6 2 3
10
85 195 5 39 3 13 266 154 14 2

Sample Output:

2
0
1
2

Note:

In the first test case if we remove the vertices with values $$$1$$$ and $$$2$$$ we will obtain a bipartite graph, so the answer is $$$2$$$, it is impossible to remove less than $$$2$$$ vertices and still obtain a bipartite graph.

Before	After

test case #1

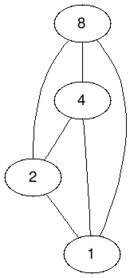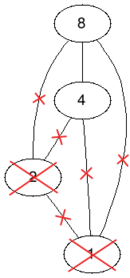In the second test case we do not have to remove any vertex because the graph is already bipartite, so the answer is $$$0$$$.

Before	After

test case #2

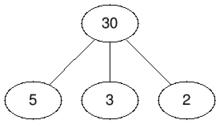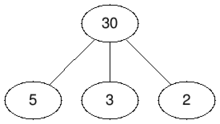In the third test case we only have to remove the vertex with value $$$12$$$, so the answer is $$$1$$$.

Before	After

test case #3

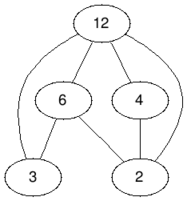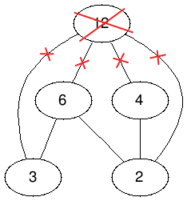In the fourth test case we remove the vertices with values $$$2$$$ and $$$195$$$, so the answer is $$$2$$$.

Before	After

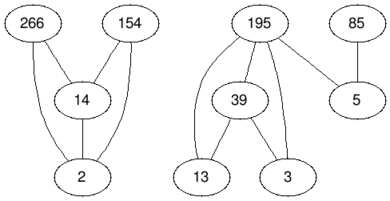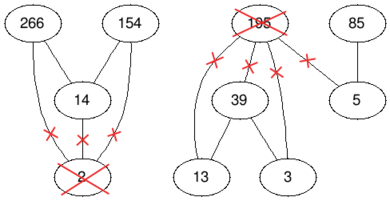test case #4