Preparando MOJI
This version of the problem differs from the previous one only in the constraint on $$$n$$$.
A tree is a connected undirected graph without cycles. A weighted tree has a weight assigned to each edge. The distance between two vertices is the minimum sum of weights on the path connecting them.
You are given a weighted tree with $$$n$$$ vertices, each edge has a weight of $$$1$$$. Denote $$$d(v)$$$ as the distance between vertex $$$1$$$ and vertex $$$v$$$.
Let $$$f(x)$$$ be the minimum possible value of $$$\max\limits_{1 \leq v \leq n} \ {d(v)}$$$ if you can temporarily add an edge with weight $$$x$$$ between any two vertices $$$a$$$ and $$$b$$$ $$$(1 \le a, b \le n)$$$. Note that after this operation, the graph is no longer a tree.
For each integer $$$x$$$ from $$$1$$$ to $$$n$$$, find $$$f(x)$$$.
The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases.
The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 3 \cdot 10^5$$$).
Each of the next $$$n−1$$$ lines contains two integers $$$u$$$ and $$$v$$$ ($$$1 \le u,v \le n$$$) indicating that there is an edge between vertices $$$u$$$ and $$$v$$$. It is guaranteed that the given edges form a tree.
It is guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$3 \cdot 10^5$$$.
For each test case, print $$$n$$$ integers in a single line, $$$x$$$-th of which is equal to $$$f(x)$$$ for all $$$x$$$ from $$$1$$$ to $$$n$$$.
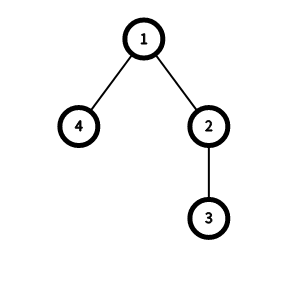
341 22 31 421 271 21 33 43 53 65 7
1 2 2 2 1 1 2 2 3 3 3 3 3