Preparando MOJI
You found a painting on a canvas of size $$$n \times m$$$. The canvas can be represented as a grid with $$$n$$$ rows and $$$m$$$ columns. Each cell has some color. Cell $$$(i, j)$$$ has color $$$c_{i,j}$$$.
Near the painting you also found a brush in the shape of a $$$2 \times 2$$$ square, so the canvas was surely painted in the following way: initially, no cell was painted. Then, the following painting operation has been performed some number of times:
All cells must be painted at least once. A cell can be painted multiple times. In this case, its final color will be the last one.
Find any sequence of at most $$$nm$$$ operations that could have led to the painting you found or state that it's impossible.
The first line of input contains two integers $$$n$$$ and $$$m$$$ ($$$2 \le n, m \le 1000$$$) — the dimensions of the canvas.
On the $$$i$$$-th of the next $$$n$$$ lines of input, there will be $$$m$$$ integers. The $$$j$$$-th of them is $$$a_{i,j}$$$ ($$$1 \le a_{i,j} \le nm$$$) — the color of cell $$$(i, j)$$$.
If there is no solution, print a single integer $$$-1$$$.
Otherwise, on the first line, print one integer $$$q$$$ ($$$1 \le q \le nm$$$) — the number of operations.
Next, print the operations in order. On the $$$k$$$-th of the next $$$q$$$ lines, print three integers $$$i$$$, $$$j$$$, $$$c$$$ ($$$1 \le i < n$$$, $$$1 \le j < m$$$, $$$1 \le c \le nm$$$) — the description of the $$$k$$$-th operation.
If there are multiple solutions, print any.
4 4 5 5 3 3 1 1 5 3 2 2 5 4 2 2 4 4
6 1 3 3 3 3 4 2 2 5 1 1 5 2 1 1 3 1 2
3 4 1 1 1 1 2 2 3 1 2 2 1 1
-1
In the first test case, the solution is not unique. Here's one of them:
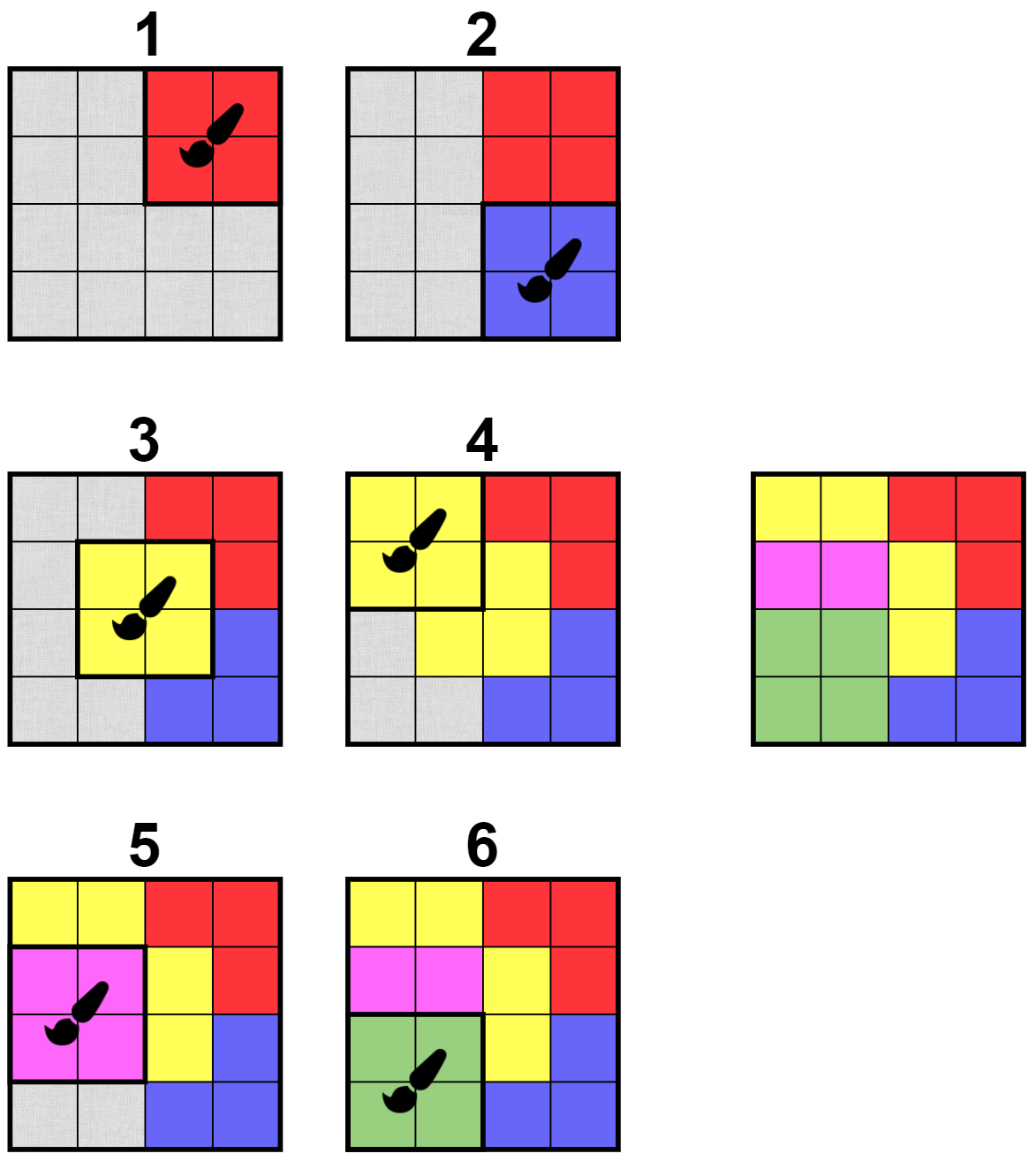
In the second test case, there is no way one could obtain the given painting, thus the answer is $$$-1$$$.
Informação
Provedor Codeforces
Código CF1638D
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 10:22:20
Relacionados