Preparando MOJI
You have a rectangular board of size $$$n\times m$$$ ($$$n$$$ rows, $$$m$$$ columns). The $$$n$$$ rows are numbered from $$$1$$$ to $$$n$$$ from top to bottom, and the $$$m$$$ columns are numbered from $$$1$$$ to $$$m$$$ from left to right.
The cell at the intersection of row $$$i$$$ and column $$$j$$$ contains the number $$$i^j$$$ ($$$i$$$ raised to the power of $$$j$$$). For example, if $$$n=3$$$ and $$$m=3$$$ the board is as follows:
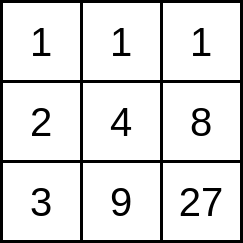
Find the number of distinct integers written on the board.
The only line contains two integers $$$n$$$ and $$$m$$$ ($$$1\le n,m\le 10^6$$$) — the number of rows and columns of the board.
Print one integer, the number of distinct integers on the board.
3 3
7
2 4
5
4 2
6
The statement shows the board for the first test case. In this case there are $$$7$$$ distinct integers: $$$1$$$, $$$2$$$, $$$3$$$, $$$4$$$, $$$8$$$, $$$9$$$, and $$$27$$$.
In the second test case, the board is as follows:
There are $$$5$$$ distinct numbers: $$$1$$$, $$$2$$$, $$$4$$$, $$$8$$$ and $$$16$$$.
In the third test case, the board is as follows:
There are $$$6$$$ distinct numbers: $$$1$$$, $$$2$$$, $$$3$$$, $$$4$$$, $$$9$$$ and $$$16$$$.
Informação
Provedor Codeforces
Código CF1646E
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 10:22:45
Relacionados