Preparando MOJI
After the most stunning success with the fifth-graders, Madoka has been trusted with teaching the sixth-graders.
There's $$$n$$$ single-place desks in her classroom. At the very beginning Madoka decided that the student number $$$b_i$$$ ($$$1 \le b_i \le n$$$) will sit at the desk number $$$i$$$. Also there's an infinite line of students with numbers $$$n + 1, n + 2, n + 3, \ldots$$$ waiting at the door with the hope of being able to learn something from the Madoka herself. Pay attention that each student has his unique number.
After each lesson, the following happens in sequence.
Note that in the end there is exactly one student at each desk again. It is guaranteed that the numbers $$$p$$$ are such that at least one student is removed after each lesson. Check out the explanation to the first example for a better understanding.
After several (possibly, zero) lessons the desk $$$i$$$ is occupied by student $$$a_i$$$. Given the values $$$a_1, a_2, \ldots, a_n$$$ and $$$p_1, p_2, \ldots, p_n$$$, find the lexicographically smallest suitable initial seating permutation $$$b_1, b_2, \ldots, b_n$$$.
The permutation is an array of $$$n$$$ different integers from $$$1$$$ up to $$$n$$$ in any order. For example, $$$[2,3,1,5,4]$$$ is a permutation, but $$$[1,2,2]$$$ is not ($$$2$$$ occurs twice). $$$[1,3,4]$$$ is not a permutation either ($$$n=3$$$ but there's $$$4$$$ in the array).
For two different permutations $$$a$$$ and $$$b$$$ of the same length, $$$a$$$ is lexicographically less than $$$b$$$ if in the first position where $$$a$$$ and $$$b$$$ differ, the permutation $$$a$$$ has a smaller element than the corresponding element in $$$b$$$.
The first line of input data contains an integer $$$n$$$ ($$$2 \le n \le 10^5$$$) — a number of desks in the classroom.
The second line contains $$$n$$$ integers $$$p_1, p_2, \ldots, p_n$$$ ($$$1 \leq p_i \leq n$$$) — desks where the students move. It is guaranteed that $$$p$$$ has at least two equal elements.
The third line contains $$$n$$$ integers $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \leq a_i \leq 10^9$$$) — the final seating of the students. It is guaranteed that there is an initial permutation from which the seating $$$a$$$ can be obtained.
In the only line print $$$n$$$ integers $$$b_1, b_2, \ldots, b_n$$$ ($$$1 \le b_i \le n$$$) — lexicographically minimum permutation describing the initial seating of the sixth-graders that can lead to the final seating $$$a$$$.
5 5 5 3 3 1 1 8 2 9 4
1 3 2 5 4
5 1 3 2 5 2 3 2 5 4 1
3 2 5 4 1
10 10 8 5 3 7 8 6 6 1 1 5 26 24 27 21 4 18 2 28 1
5 4 2 6 7 8 3 9 1 10
The description of the first test is below:
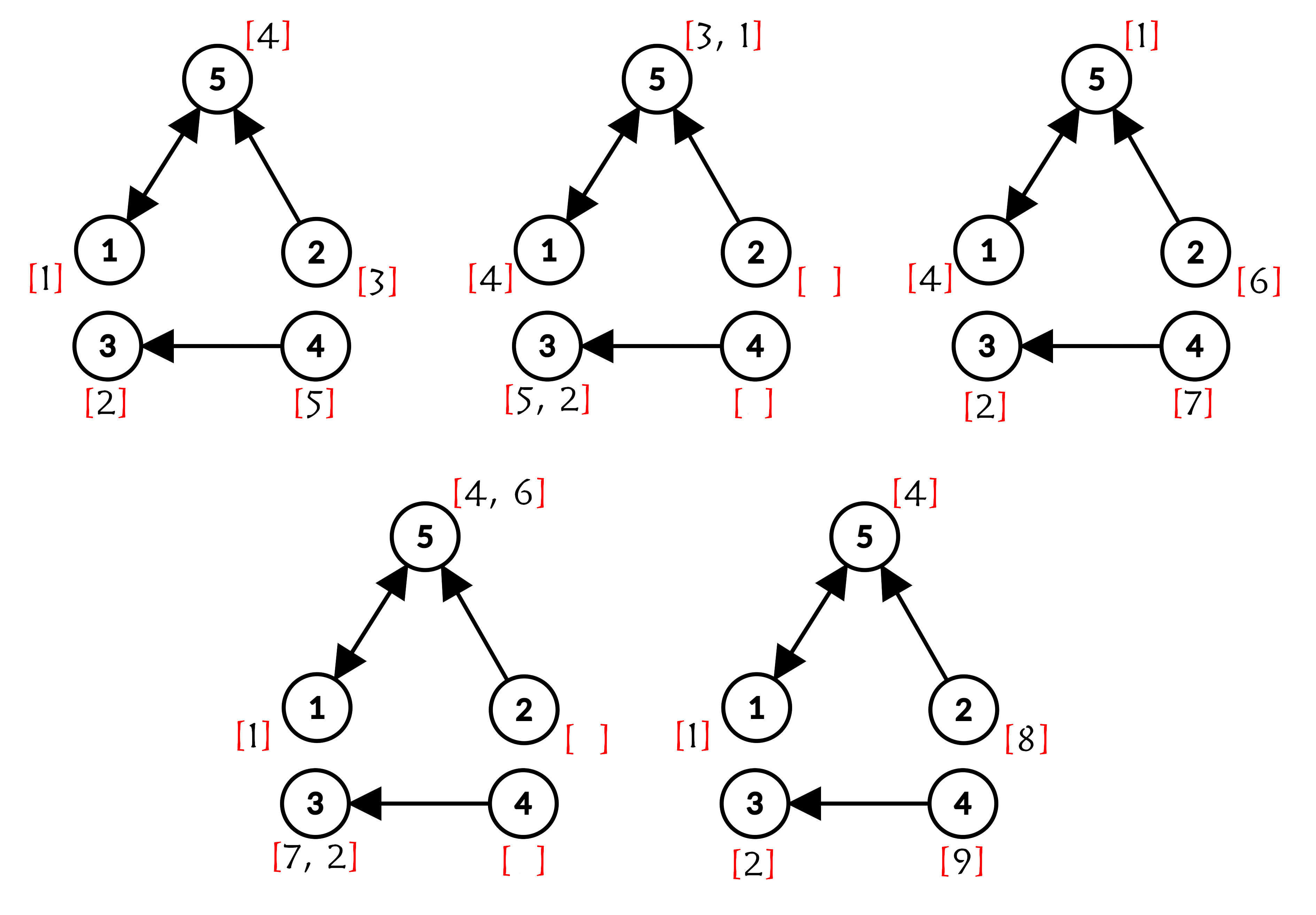
The first picture shows the starting permutation, which is the answer. Then the students sitting at desks $$$1, 2$$$ are transferred to a $$$5$$$ desk. Also, a $$$1$$$ student moved from a $$$5$$$ desk, and a student from a $$$4$$$ disk is transferred to a $$$3$$$ desk.
Thus, after all these transfers permutation shown in the second image is obtained. Then, at the desk with the number $$$5$$$, the student with the number $$$3$$$ is expelled, and at the desk with the number $$$3$$$, the student with the number $$$5$$$ is expelled. (Since their numbers are not the smallest) Then new students with numbers $$$6, 7$$$ sit at desks numbered $$$2, 4$$$. And this permutation (after the end of the first lesson) is shown in the third image.
The $$$4$$$ image shows the seating arrangement, after the second lesson before all the extra ones were kicked out. And the fifth shows the final seating after $$$2$$$ lesson.