Preparando MOJI
Polycarpus has many tasks. Each task is characterized by three integers li, ri and ti. Three integers (li, ri, ti) mean that to perform task i, one needs to choose an integer si (li ≤ si; si + ti - 1 ≤ ri), then the task will be carried out continuously for ti units of time, starting at time si and up to time si + ti - 1, inclusive. In other words, a task is performed for a continuous period of time lasting ti, should be started no earlier than li, and completed no later than ri.
Polycarpus's tasks have a surprising property: for any task j, k (with j < k) lj < lk and rj < rk.
Let's suppose there is an ordered set of tasks A, containing |A| tasks. We'll assume that aj = (lj, rj, tj) (1 ≤ j ≤ |A|). Also, we'll assume that the tasks are ordered by increasing lj with the increase in number.
Let's consider the following recursive function f, whose argument is an ordered set of tasks A, and the result is an integer. The function f(A) is defined by the greedy algorithm, which is described below in a pseudo-language of programming.
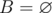 , ans = 0.
, ans = 0. 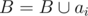 . Go to the next task (step 3).
. Go to the next task (step 3). 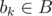 , that first, task ai can be done at time si = max
, that first, task ai can be done at time si = max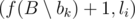 , and secondly, the value of
, and secondly, the value of 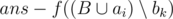 is positive and takes the maximum value among all bk that satisfy the first condition. If you can choose multiple tasks as bk, choose the one with the maximum number in set A.
is positive and takes the maximum value among all bk that satisfy the first condition. If you can choose multiple tasks as bk, choose the one with the maximum number in set A. 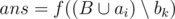 ,
, 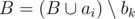 . Go to the next task (step 3).
. Go to the next task (step 3). Polycarpus got entangled in all these formulas and definitions, so he asked you to simulate the execution of the function f, calculate the value of f(A).
The first line of the input contains a single integer n (1 ≤ n ≤ 105) — the number of tasks in set A.
Then n lines describe the tasks. The i-th line contains three space-separated integers li, ri, ti (1 ≤ li ≤ ri ≤ 109, 1 ≤ ti ≤ ri - li + 1) — the description of the i-th task.
It is guaranteed that for any tasks j, k (considering that j < k) the following is true: lj < lk and rj < rk.
For each task i print a single integer — the result of processing task i on the i-th iteration of the cycle (step 3) in function f(A). In the i-th line print:
5
1 8 5
2 9 3
3 10 3
8 11 4
11 12 2
0 0 1 0 -1
13
1 8 5
2 9 4
3 10 1
4 11 3
8 12 5
9 13 5
10 14 5
11 15 1
12 16 1
13 17 1
14 18 3
15 19 3
16 20 2
0 0 0 2 -1 -1 0 0 0 0 7 0 12