Preparando MOJI
You are given three points on a plane. You should choose some segments on the plane that are parallel to coordinate axes, so that all three points become connected. The total length of the chosen segments should be the minimal possible.
Two points $$$a$$$ and $$$b$$$ are considered connected if there is a sequence of points $$$p_0 = a, p_1, \ldots, p_k = b$$$ such that points $$$p_i$$$ and $$$p_{i+1}$$$ lie on the same segment.
The input consists of three lines describing three points. Each line contains two integers $$$x$$$ and $$$y$$$ separated by a space — the coordinates of the point ($$$-10^9 \le x, y \le 10^9$$$). The points are pairwise distinct.
On the first line output $$$n$$$ — the number of segments, at most 100.
The next $$$n$$$ lines should contain descriptions of segments. Output four integers $$$x_1$$$, $$$y_1$$$, $$$x_2$$$, $$$y_2$$$ on a line — the coordinates of the endpoints of the corresponding segment ($$$-10^9 \le x_1, y_1, x_2, y_2 \le 10^9$$$). Each segment should be either horizontal or vertical.
It is guaranteed that the solution with the given constraints exists.
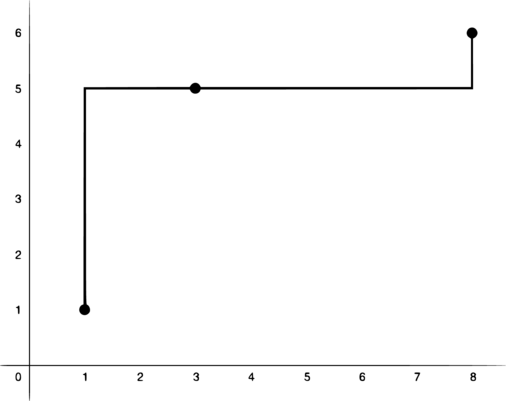
1 1 3 5 8 6
3 1 1 1 5 1 5 8 5 8 5 8 6
The points and the segments from the example are shown below.
Informação
Provedor Codeforces
Código CF1666C
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 10:26:26
Relacionados