Lenient Vertex Cover

Description:

Input:

The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of testcases.

The first line of each testcase contains two integers $$$n$$$ and $$$m$$$ ($$$2 \le n \le 10^6$$$; $$$n - 1 \le m \le \min(10^6, \frac{n \cdot (n - 1)}{2})$$$) — the number of vertices and the number of edges of the graph.

Each of the next $$$m$$$ lines contains two integers $$$v$$$ and $$$u$$$ ($$$1 \le v, u \le n$$$; $$$v \neq u$$$) — the descriptions of the edges.

For each testcase, the graph is connected and doesn't have multiple edges. The sum of $$$n$$$ over all testcases doesn't exceed $$$10^6$$$. The sum of $$$m$$$ over all testcases doesn't exceed $$$10^6$$$.

Output:

For each testcase, the first line should contain YES if a lenient vertex cover exists, and NO otherwise. If it exists, the second line should contain a binary string $$$s$$$ of length $$$n$$$, where $$$s_i = 1$$$ means that vertex $$$i$$$ is in the vertex cover, and $$$s_i = 0$$$ means that vertex $$$i$$$ isn't.

If there are multiple answers, then print any of them.

Sample Input:

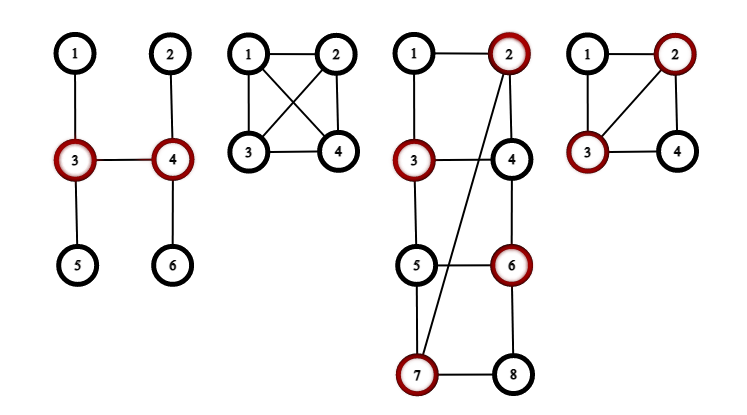
4
6 5
1 3
2 4
3 4
3 5
4 6
4 6
1 2
2 3
3 4
1 4
1 3
2 4
8 11
1 3
2 4
3 5
4 6
5 7
6 8
1 2
3 4
5 6
7 8
7 2
4 5
1 2
2 3
3 4
1 3
2 4

Sample Output:

YES
001100
NO
YES
01100110
YES
0110

Sample Input:

1
10 15
9 4
3 4
6 4
1 2
8 2
8 3
7 2
9 5
7 8
5 10
1 4
2 10
5 3
5 7
2 9

Sample Output:

YES
0101100100

Sample Input:

1
10 19
7 9
5 3
3 4
1 6
9 4
1 4
10 5
7 1
9 2
8 3
7 3
10 9
2 10
9 8
3 2
1 5
10 7
9 5
1 2

Sample Output:

YES
1010000011

Note:

Here are the graphs from the first example. The vertices in the lenient vertex covers are marked red.