Number of Groups

Description:

Input:

Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^5$$$). Description of the test cases follows.

The first line of each test case contains a single integer $$$n$$$ ($$$1 \leq n \leq 10^5$$$) — the number of segments.

Each of the next $$$n$$$ lines contains three integers $$$c_i, l_i, r_i$$$ ($$$0 \leq c_i \leq 1, 0 \leq l_i \leq r_i \leq 10^9$$$), describing the $$$i$$$-th segment.

It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$10^5$$$.

Output:

For each test case, print a single integer $$$k$$$, the number of groups of segments.

Sample Input:

2
5
0 0 5
1 2 12
0 4 7
1 9 16
0 13 19
3
1 0 1
1 1 2
0 3 4

Sample Output:

2
3

Note:

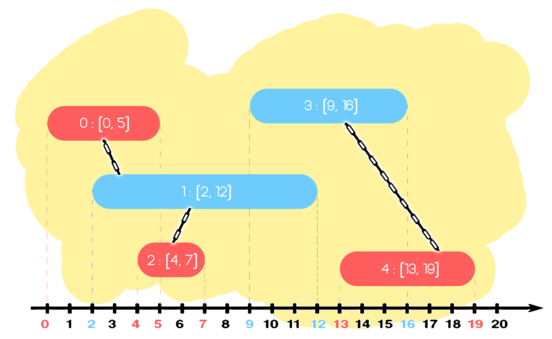
In the first example there are $$$5$$$ segments. The segments $$$1$$$ and $$$2$$$ are connected, because they are of different colors and share a point. Also, the segments $$$2$$$ and $$$3$$$ are connected, and so are segments $$$4$$$ and $$$5$$$. Thus, there are two groups: one containing segments $$$\{1, 2, 3\}$$$, and the other one containing segments $$$\{4, 5\}$$$.