Mirror Grid

2000ms

262144K

Description:

You are given a square grid with $$$n$$$ rows and $$$n$$$ columns. Each cell contains either $$$0$$$ or $$$1$$$.

In an operation, you can select a cell of the grid and flip it (from $$$0 \to 1$$$ or $$$1 \to 0$$$). Find the minimum number of operations you need to obtain a square that remains the same when rotated $$$0^{\circ}$$$, $$$90^{\circ}$$$, $$$180^{\circ}$$$ and $$$270^{\circ}$$$.

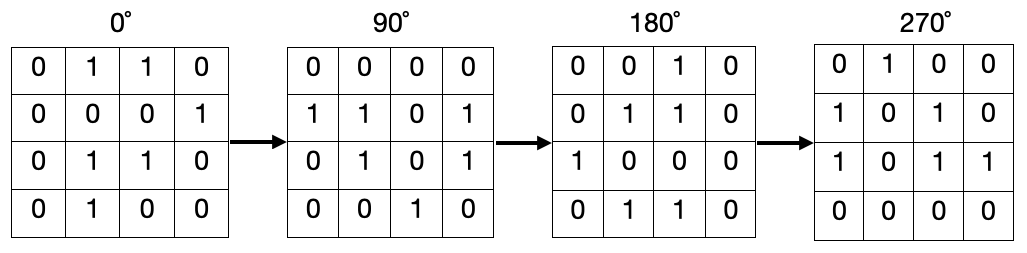
The picture below shows an example of all rotations of a grid.

$\text{[math]}$

Input:

The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 100$$$) — the number of test cases.

The first line of each test case contains a single integer $$$n$$$ ($$$1 \leq n \leq 100$$$) — the size of the grid.

Then $$$n$$$ lines follow, each with $$$n$$$ characters $$$a_{i,j}$$$ ($$$0 \leq a_{i,j} \leq 1$$$) — the number written in each cell.

Output:

For each test case output a single integer — the minimum number of operations needed to make the square look the same rotated $$$0^{\circ}$$$, $$$90^{\circ}$$$, $$$180^{\circ}$$$ and $$$270^{\circ}$$$.

Sample Input:

Sample Output:

Note:

In the first test case, we can perform one operations to make the grid $$$\begin{matrix}0 & 1 & 0\\ 1 & 1 & \color{red}{1}\\ 0 & 1 & 0\end{matrix}$$$. Now, all rotations of the square are the same.

In the second test case, all rotations of the square are already the same, so we don't need any flips.

Informação

Provedor Codeforces

Código CF1703E