Making Towers

1000ms

262144K

Description:

You have a sequence of $$$n$$$ colored blocks. The color of the $$$i$$$-th block is $$$c_i$$$, an integer between $$$1$$$ and $$$n$$$.

You will place the blocks down in sequence on an infinite coordinate grid in the following way.

Initially, you place block $$$1$$$ at $$$(0, 0)$$$.
For $$$2 \le i \le n$$$, if the $$$(i - 1)$$$-th block is placed at position $$$(x, y)$$$, then the $$$i$$$-th block can be placed at one of positions $$$(x + 1, y)$$$, $$$(x - 1, y)$$$, $$$(x, y + 1)$$$ (but not at position $$$(x, y - 1)$$$), as long no previous block was placed at that position.

A tower is formed by $$$s$$$ blocks such that they are placed at positions $$$(x, y), (x, y + 1), \ldots, (x, y + s - 1)$$$ for some position $$$(x, y)$$$ and integer $$$s$$$. The size of the tower is $$$s$$$, the number of blocks in it. A tower of color $$$r$$$ is a tower such that all blocks in it have the color $$$r$$$.

For each color $$$r$$$ from $$$1$$$ to $$$n$$$, solve the following problem independently:

Find the maximum size of a tower of color $$$r$$$ that you can form by placing down the blocks according to the rules.

Input:

The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases.

The first line of each test case contains a single integer $$$n$$$ ($$$1 \le n \le 10^5$$$).

The second line of each test case contains $$$n$$$ integers $$$c_1, c_2, \ldots, c_n$$$ ($$$1 \le c_i \le n$$$).

It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.

Output:

For each test case, output $$$n$$$ integers. The $$$r$$$-th of them should be the maximum size of an tower of color $$$r$$$ you can form by following the given rules. If you cannot form any tower of color $$$r$$$, the $$$r$$$-th integer should be $$$0$$$.

Sample Input:

6
7
1 2 3 1 2 3 1
6
4 2 2 2 4 4
1
1
5
5 4 5 3 5
6
3 3 3 1 3 3
8
1 2 3 4 4 3 2 1

Sample Output:

3 2 2 0 0 0 0 
0 3 0 2 0 0 
1 
0 0 1 1 1 
1 0 4 0 0 0 
2 2 2 2 0 0 0 0

Note:

In the first test case, one of the possible ways to form a tower of color $$$1$$$ and size $$$3$$$ is:

place block $$$1$$$ at position $$$(0, 0)$$$;
place block $$$2$$$ to the right of block $$$1$$$, at position $$$(1, 0)$$$;
place block $$$3$$$ above block $$$2$$$, at position $$$(1, 1)$$$;
place block $$$4$$$ to the left of block $$$3$$$, at position $$$(0, 1)$$$;
place block $$$5$$$ to the left of block $$$4$$$, at position $$$(-1, 1)$$$;
place block $$$6$$$ above block $$$5$$$, at position $$$(-1, 2)$$$;
place block $$$7$$$ to the right of block $$$6$$$, at position $$$(0, 2)$$$.

$\text{[math]}$

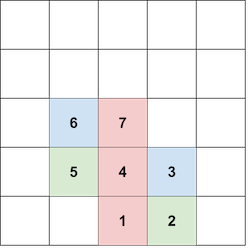
The blocks at positions $$$(0, 0)$$$, $$$(0, 1)$$$, and $$$(0, 2)$$$ all have color $$$1$$$, forming an tower of size $$$3$$$.

In the second test case, note that the following placement is not valid, since you are not allowed to place block $$$6$$$ under block $$$5$$$:

$\text{[math]}$

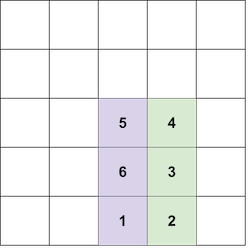
It can be shown that it is impossible to form a tower of color $$$4$$$ and size $$$3$$$.

Informação

Provedor Codeforces

Código CF1706B