Qpwoeirut And The City

Description:

Input:

The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases.

The first line of each test case contains the single integer $$$n$$$ ($$$3 \le n \le 10^5$$$) — the number of buildings in Qpwoeirut's city.

The second line of each test case contains $$$n$$$ integers $$$h_1, h_2, \ldots, h_n$$$ ($$$1 \le h_i \le 10^9$$$) — the number of floors in each of the buildings of the city.

It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.

Output:

For each test case, print a single integer — the minimum number of additional floors Qpwoeirut needs to build in order to maximize the number of cool buildings.

Sample Input:

6
3
2 1 2
5
1 2 1 4 3
6
3 1 4 5 5 2
8
4 2 1 3 5 3 6 1
6
1 10 1 1 10 1
8
1 10 11 1 10 11 10 1

Sample Output:

2
0
3
3
0
4

Note:

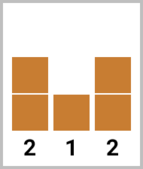
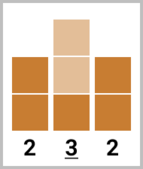
In the first test case, it is optimal for Qpwoeirut to make the second building cool by building $$$2$$$ additional floors on top of it, making it taller than both of its adjacent buildings. The final heights of buildings will be $$$[2, \underline{3}, 2]$$$.

In the second test case, the number of cool buildings is already maximized, so Qpwoeirut does not need to do anything.

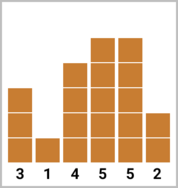
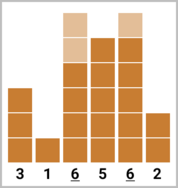
In the third test case, it is optimal for Qpwoeirut to make the third and fifth buildings cool by building $$$2$$$ additional floors onto the third building and $$$1$$$ additional floor onto the fifth building. The final heights of buildings will be $$$[3, 1, \underline{6}, 5, \underline{6}, 2]$$$.

It can be shown that it is impossible to make more than $$$2$$$ of the buildings cool, or to make $$$2$$$ buildings cool using fewer than $$$3$$$ additional floors.

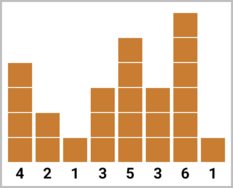
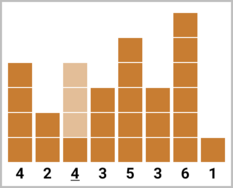
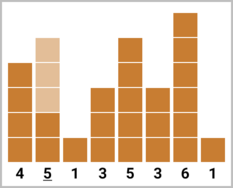
In the fourth test case, Qpwoeirut can either make the second building cool, or he can make the third building cool. Either way, he will be building $$$3$$$ additional floors and maximizing the number of cool buildings. The final heights of buildings will be $$$[4, 2, \underline{4}, 3, 5, 3, 6, 1]$$$ or $$$[4, \underline{5}, 1, 3, 5, 3, 6, 1]$$$.