Rain

Description:

Input:

Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \leq t \leq 10^4$$$). The description of the test cases follows.

The first line of each test case contains two integers $$$n$$$ and $$$m$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$, $$$1 \leq m \leq 10^9$$$) — the number of rainy days and the maximal accumulated rainfall with no flood occurring.

Then $$$n$$$ lines follow. The $$$i$$$-th of these lines contains two integers $$$x_i$$$ and $$$p_i$$$ ($$$1 \leq x_i,p_i \leq 10^9$$$) — the position and intensity of the $$$i$$$-th day's rain.

The sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.

Output:

For each test case, output a binary string $$$s$$$ length of $$$n$$$. The $$$i$$$-th character of $$$s$$$ is 1 if after erasing the $$$i$$$-th day's rain there is no flood, while it is 0, if after erasing the $$$i$$$-th day's rain the flood still happens.

Sample Input:

4
3 6
1 5
5 5
3 4
2 3
1 3
5 2
2 5
1 6
10 6
6 12
4 5
1 6
12 5
5 5
9 7
8 3

Sample Output:

001
11
00
100110

Note:

In the first test case, if we do not use the spell, the accumulated rainfall distribution will be like this:

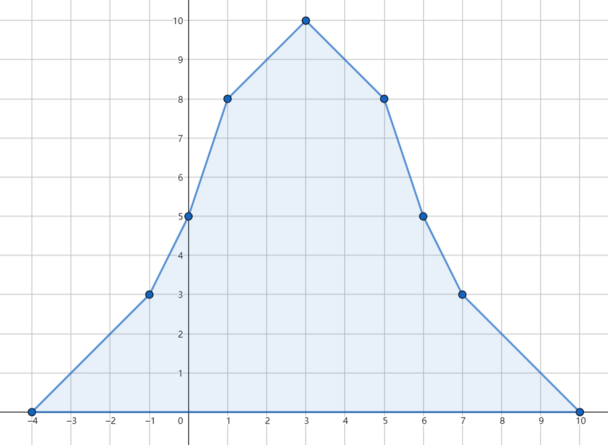
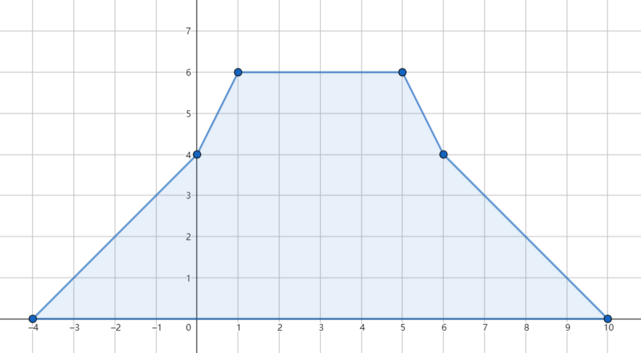
If we erase the third day's rain, the flood is avoided and the accumulated rainfall distribution looks like this:

In the second test case, since initially the flood will not happen, we can erase any day's rain.

In the third test case, there is no way to avoid the flood.