Description:
You are given a rooted tree. It contains $$$n$$$ vertices, which are numbered from $$$1$$$ to $$$n$$$. The root is the vertex $$$1$$$.
Each edge has two positive integer values. Thus, two positive integers $$$a_j$$$ and $$$b_j$$$ are given for each edge.
Output $$$n-1$$$ numbers $$$r_2, r_3, \dots, r_n$$$, where $$$r_i$$$ is defined as follows.
Consider the path from the root (vertex $$$1$$$) to $$$i$$$ ($$$2 \le i \le n$$$). Let the sum of the costs of $$$a_j$$$ along this path be $$$A_i$$$. Then $$$r_i$$$ is equal to the length of the maximum prefix of this path such that the sum of $$$b_j$$$ along this prefix does not exceed $$$A_i$$$.
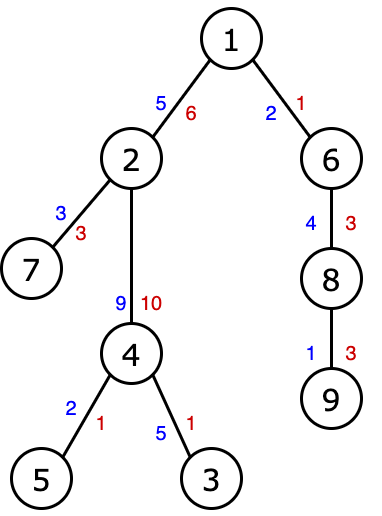Example for $$$n=9$$$. The blue color shows the costs of $$$a_j$$$, and the red color shows the costs of $$$b_j$$$. Consider an example. In this case:
- $$$r_2=0$$$, since the path to $$$2$$$ has an amount of $$$a_j$$$ equal to $$$5$$$, only the prefix of this path of length $$$0$$$ has a smaller or equal amount of $$$b_j$$$;
- $$$r_3=3$$$, since the path to $$$3$$$ has an amount of $$$a_j$$$ equal to $$$5+9+5=19$$$, the prefix of length $$$3$$$ of this path has a sum of $$$b_j$$$ equal to $$$6+10+1=17$$$ ( the number is $$$17 \le 19$$$);
- $$$r_4=1$$$, since the path to $$$4$$$ has an amount of $$$a_j$$$ equal to $$$5+9=14$$$, the prefix of length $$$1$$$ of this path has an amount of $$$b_j$$$ equal to $$$6$$$ (this is the longest suitable prefix, since the prefix of length $$$2$$$ already has an amount of $$$b_j$$$ equal to $$$6+10=16$$$, which is more than $$$14$$$);
- $$$r_5=2$$$, since the path to $$$5$$$ has an amount of $$$a_j$$$ equal to $$$5+9+2=16$$$, the prefix of length $$$2$$$ of this path has a sum of $$$b_j$$$ equal to $$$6+10=16$$$ (this is the longest suitable prefix, since the prefix of length $$$3$$$ already has an amount of $$$b_j$$$ equal to $$$6+10+1=17$$$, what is more than $$$16$$$);
- $$$r_6=1$$$, since the path up to $$$6$$$ has an amount of $$$a_j$$$ equal to $$$2$$$, the prefix of length $$$1$$$ of this path has an amount of $$$b_j$$$ equal to $$$1$$$;
- $$$r_7=1$$$, since the path to $$$7$$$ has an amount of $$$a_j$$$ equal to $$$5+3=8$$$, the prefix of length $$$1$$$ of this path has an amount of $$$b_j$$$ equal to $$$6$$$ (this is the longest suitable prefix, since the prefix of length $$$2$$$ already has an amount of $$$b_j$$$ equal to $$$6+3=9$$$, which is more than $$$8$$$);
- $$$r_8=2$$$, since the path up to $$$8$$$ has an amount of $$$a_j$$$ equal to $$$2+4=6$$$, the prefix of length $$$2$$$ of this path has an amount of $$$b_j$$$ equal to $$$1+3=4$$$;
- $$$r_9=3$$$, since the path to $$$9$$$ has an amount of $$$a_j$$$ equal to $$$2+4+1=7$$$, the prefix of length $$$3$$$ of this path has a sum of $$$b_j$$$ equal to $$$1+3+3=7$$$.
Input:
The first line contains an integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases in the test.
The descriptions of test cases follow.
Each description begins with a line that contains an integer $$$n$$$ ($$$2 \le n \le 2\cdot10^5$$$) — the number of vertices in the tree.
This is followed by $$$n-1$$$ string, each of which contains three numbers $$$p_j, a_j, b_j$$$ ($$$1 \le p_j \le n$$$; $$$1 \le a_j,b_j \le 10^9$$$) — the ancestor of the vertex $$$j$$$, the first and second values an edge that leads from $$$p_j$$$ to $$$j$$$. The value of $$$j$$$ runs through all values from $$$2$$$ to $$$n$$$ inclusive. It is guaranteed that each set of input data has a correct hanged tree with a root at the vertex $$$1$$$.
It is guaranteed that the sum of $$$n$$$ over all input test cases does not exceed $$$2\cdot10^5$$$.
Output:
For each test case, output $$$n-1$$$ integer in one line: $$$r_2, r_3, \dots, r_n$$$.
Sample Input:
4
9
1 5 6
4 5 1
2 9 10
4 2 1
1 2 1
2 3 3
6 4 3
8 1 3
4
1 1 100
2 1 1
3 101 1
4
1 100 1
2 1 1
3 1 101
10
1 1 4
2 3 5
2 5 1
3 4 3
3 1 5
5 3 5
5 2 1
1 3 2
6 2 1
Sample Output:
0 3 1 2 1 1 2 3
0 0 3
1 2 2
0 1 2 1 1 2 2 1 1
Note:
The first example is clarified in the statement.
In the second example:
- $$$r_2=0$$$, since the path to $$$2$$$ has an amount of $$$a_j$$$ equal to $$$1$$$, only the prefix of this path of length $$$0$$$ has a smaller or equal amount of $$$b_j$$$;
- $$$r_3=0$$$, since the path to $$$3$$$ has an amount of $$$a_j$$$ equal to $$$1+1=2$$$, the prefix of length $$$1$$$ of this path has an amount of $$$b_j$$$ equal to $$$100$$$ ($$$100 > 2$$$);
- $$$r_4=3$$$, since the path to $$$4$$$ has an amount of $$$a_j$$$ equal to $$$1+1+101=103$$$, the prefix of length $$$3$$$ of this path has an amount of $$$b_j$$$ equal to $$$102$$$, .
