Preparando MOJI
This is an interactive problem.
I want to play a game with you...
We hid from you a cyclic graph of $$$n$$$ vertices ($$$3 \le n \le 10^{18}$$$). A cyclic graph is an undirected graph of $$$n$$$ vertices that form one cycle. Each vertex belongs to the cycle, i.e. the length of the cycle (the number of edges in it) is exactly $$$n$$$. The order of the vertices in the cycle is arbitrary.
You can make queries in the following way:
You win if you guess the number of vertices in the hidden graph (number $$$n$$$) by making no more than $$$50$$$ queries.
Note that the interactor is implemented in such a way that for any ordered pair $$$(a, b)$$$, it always returns the same value for query "? a b", no matter how many such queries. Note that the "? b a" query may be answered differently by the interactor.
The vertices in the graph are randomly placed, and their positions are fixed in advance.
Hacks are forbidden in this problem. The number of tests the jury has is $$$50$$$.
You can make no more than $$$50$$$ of queries. To make a query, output on a separate line:
If your program gets a number 0 as a result of a query, it means that the verdict for your solution is already defined as "wrong answer" (for example, you made more than $$$50$$$ queries or made an invalid query). In this case, your program should terminate immediately. Otherwise, in this scenario you may get a random verdict "Execution error", "Exceeded time limit" or some other verdict instead of "Wrong answer".
The answer, like queries, print on a separate line. The output of the answer is not counted as a query when counting them. To print it, use the following format:
After that, your program should terminate.
After the output of the next query, be sure to use stream cleaning functions so that some of your output is not left in some buffer. For example, in C++ you should use function flush(stdout), in Java call System.out.flush(), in Pascal flush(output) and stdout.flush() for Python.
Note that the interactor is implemented in such a way that for any ordered pair $$$(a, b)$$$, it always returns the same value for query "? a b", no matter how many such queries. Note that the "? b a" query may be answered differently by the interactor.
The vertices in the graph are randomly placed, and their positions are fixed in advance.
Hacks are forbidden in this problem. The number of tests the jury has is $$$50$$$.
1 2 -1
? 1 2 ? 1 3 ? 1 4 ! 3
In the first example, the graph could look like this
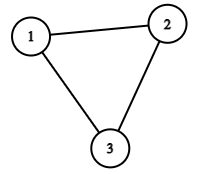
The lengths of the simple paths between all pairs of vertices in this case are $$$1$$$ or $$$2$$$.