Tea with Tangerines

Description:

Input:

The first line of the input contains a single integer $$$t$$$ ($$$1 \le t \le 100$$$) — the number of test cases. The description of test cases follows.

The first line of each test case contains the integer $$$n$$$ ($$$1 \le n \le 100$$$).

Then one line follows, containing $$$n$$$ integers $$$a_1 \le a_2 \le \ldots \le a_n$$$ ($$$1 \le a_i \le 10^7$$$).

Output:

For each test case, output a single line containing the minimum number of steps.

Sample Input:

3
5
1 2 3 4 5
1
1033
5
600 900 1300 2000 2550

Sample Output:

10
0
4

Note:

In the first test case, we initially have a piece of size $$$1$$$, so all final pieces must have size $$$1$$$. The total number of steps is: $$$0 + 1 + 2 + 3 + 4 = 10$$$.

In the second test case, we have just one piece, so we don't need to do anything, and the answer is $$$0$$$ steps.

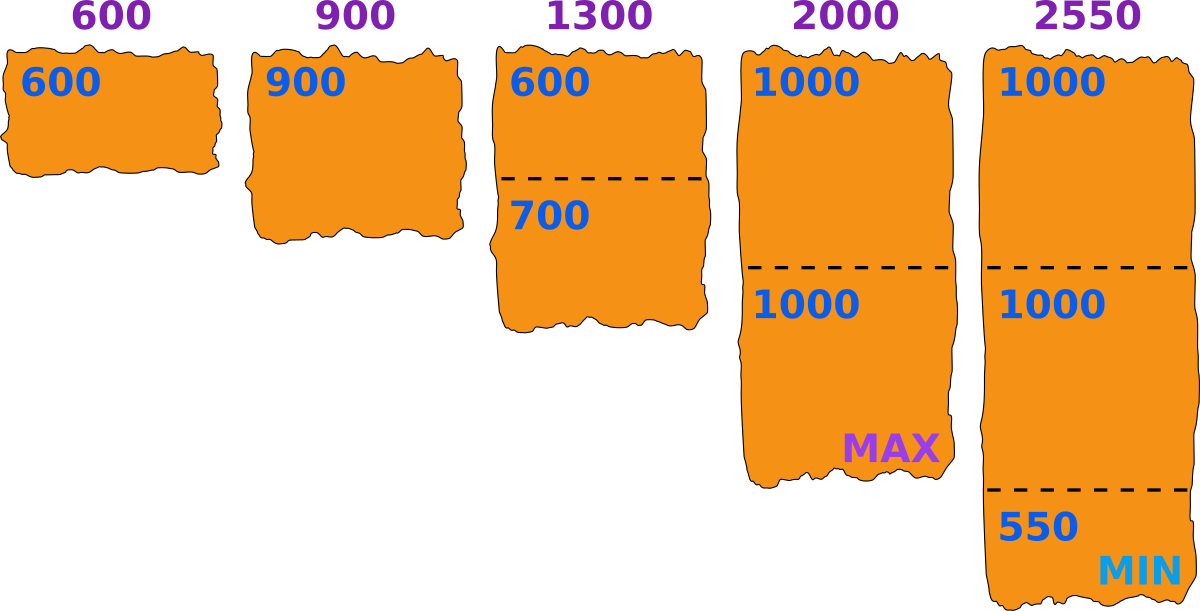
In the third test case, one of the possible cut options is: $$$600,\ 900,\ (600 | 700),\ (1000 | 1000),\ (1000 | 1000 | 550)$$$. You can see this option in the picture below. The maximum piece has size $$$1000$$$, and it is less than $$$2$$$ times bigger than the minimum piece of size $$$550$$$. $$$4$$$ steps are done. We can show that it is the minimum possible number of steps.