Preparando MOJI
 | Ela likes to go hiking a lot. She loves nature and exploring the various creatures it offers. One day, she saw a strange type of ant, with a cannibalistic feature. More specifically, an ant would eat any ants that it sees which is smaller than it. Curious about this feature from a new creature, Ela ain't furious. She conducts a long, non-dubious, sentimental experiment. |
She puts $$$n$$$ cannibalistic ants in a line on a long wooden stick. Initially, the ants have the same weight of $$$1$$$. The distance between any two consecutive ants is the same. The distance between the first ant in the line to the left end and the last ant in the line to the right end is also the same as the distance between the ants. Each ant starts moving towards the left-end or the right-end randomly and equiprobably, at the same constant pace throughout the experiment. Two ants will crash if they are standing next to each other in the line and moving in opposite directions, and ants will change direction immediately when they reach the end of the stick. Ela can't determine the moving direction of each ant, but she understands very well their behavior when crashes happen.
Please, check the example in the "Note" section, which will demonstrate the ants' behavior as above.
We can prove that after a definite amount of time, there will be only one last ant standing. Initially, each ant can randomly and equiprobably move to the left or the right, which generates $$$2^n$$$ different cases of initial movements for the whole pack. For each position in the line, calculate the probability that the ant begins in that position and survives. Output it modulo $$$10^9 + 7$$$.
Formally, let $$$M = 10^9 + 7$$$. It can be shown that the answer can be expressed as an irreducible fraction $$$\frac{p}{q}$$$, where $$$p$$$ and $$$q$$$ are integers and $$$q \not \equiv 0 \pmod{M}$$$. Output the integer equal to $$$p \cdot q^{-1} \bmod M$$$. In other words, output such an integer $$$x$$$ that $$$0 \le x < M$$$ and $$$x \cdot q \equiv p \pmod{M}$$$.
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^3$$$). The description of the test cases follows.
The only line of each test contains an integer $$$n$$$ ($$$1 \le n \le 10^6$$$) — the number of ants in the experiment.
It is guaranteed that the sum of $$$n$$$ in all tests will not exceed $$$10^6$$$.
For each test, print $$$n$$$ lines. $$$i$$$-th line contains a single number that denotes the survival probability of the $$$i$$$-th ant in the line modulo $$$10^9 + 7$$$.
3452
0 250000002 250000002 500000004 0 250000002 250000002 250000002 250000002 0 1
Here is the example of $$$6$$$ ants moving on the branch. An ant's movement will be denoted by either a character $$$L$$$ or $$$R$$$. Initially, the pack of ants on the branch will move as $$$RLRRLR$$$. Here's how the behavior of the pack demonstrated:

Initially, the ants are positioned as above.

After a while, the ant with index $$$2$$$ (walking to the left) will crash with the ant with index $$$1$$$ (walking to the right). The two ants have the same weight, therefore, ant $$$2$$$ will eat ant $$$1$$$ and gain its weight to $$$2$$$. The same thing happens with ant $$$5$$$ and ant $$$4$$$.
The ant $$$6$$$ will walk to the end of the stick, therefore changing its direction.

After that, the ant with index $$$5$$$ will crash with the ant with index $$$3$$$. Since ant $$$5$$$ is more heavy (weight=$$$2$$$) than ant $$$3$$$ (weight=$$$1$$$), ant $$$5$$$ will eat ant $$$3$$$ and gain its weight to $$$3$$$.
Ant $$$2$$$ will walk to the end of the stick, therefore changing its direction.
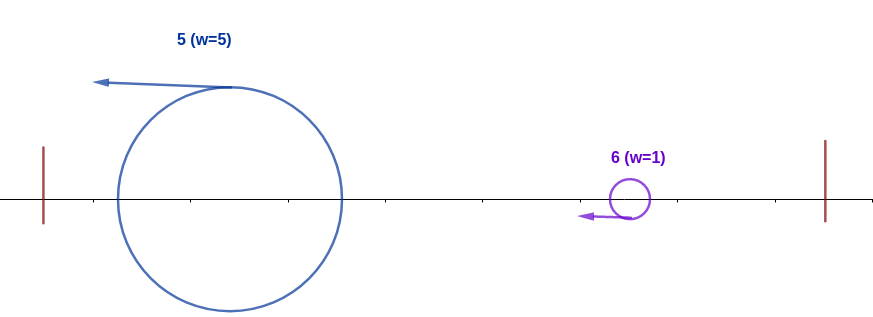
After that, the ant with index $$$5$$$ will crash with the ant with index $$$2$$$. Since ant $$$5$$$ is more heavy (weight=$$$3$$$) than ant $$$2$$$ (weight=$$$2$$$), ant $$$5$$$ will eat ant $$$2$$$ and gain its weight to $$$5$$$.
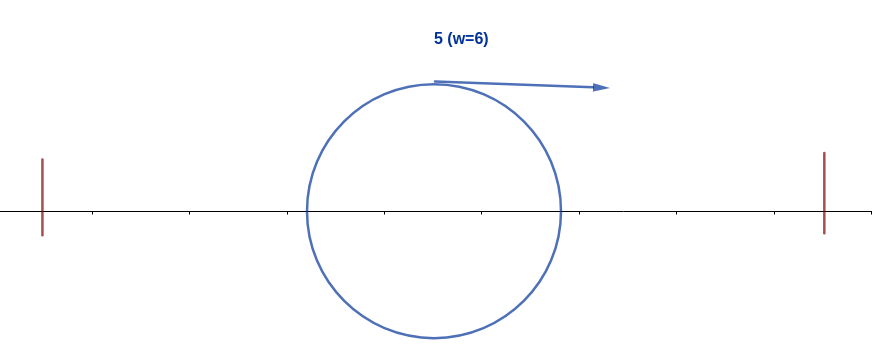
Lastly, after ant $$$5$$$ walk to the end of the branch and changes its direction, ant $$$5$$$ will eat ant $$$6$$$ and be the last ant standing.