Jumbo Extra Cheese 2

Description:

Input:

Each test contains multiple test cases. The first line contains an integer $$$t$$$ ($$$1 \leq t \leq 2 \cdot 10^4$$$) — the number of test cases. The following lines contain the description of each test case.

The first line of each test case contains an integer $$$n$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$) — the number of slices of cheese Pak Chanek has.

The $$$i$$$-th of the next $$$n$$$ lines of each test case contains two integers $$$a_i$$$ and $$$b_i$$$ ($$$1 \leq a_i,b_i \leq 10^9$$$) — the dimensions of the $$$i$$$-th slice of cheese.

It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.

Output:

For each test case, output a line containing an integer representing the minimum possible perimeter of the constructed shape.

Sample Input:

3
4
4 1
4 5
1 1
2 3
3
2 4
2 6
2 3
1
2 65

Sample Output:

26
24
134

Note:

In the first test case, a way of getting the minimum possible perimeter is to arrange the slices of cheese as follows.

We can calculate that the perimeter of the constructed shape is $$$2+5+1+1+1+1+3+1+5+1+2+3=26$$$. It can be shown that we cannot get a smaller perimeter.

Consider the following invalid arrangement.

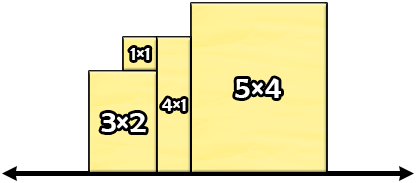
Even though the perimeter of the shape above is $$$24$$$, it does not satisfy all conditions of the problem. The bottom edge of the $$$1 \times 1$$$ slice of cheese is not a segment of the x-axis.

In the second test case, a way of getting the minimum possible perimeter is to arrange the slices of cheese as follows.

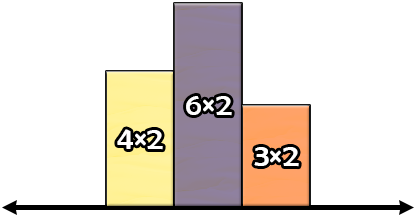
We can calculate that the perimeter of the constructed shape is $$$2+2+2+3+2+3+2+2+2+4=24$$$. It can be shown that we cannot get a smaller perimeter.