Dangerous Laser Power

4000ms

524288K

Description:

Pak Chanek has an $$$n \times m$$$ grid of portals. The portal on the $$$i$$$-th row and $$$j$$$-th column is denoted as portal $$$(i,j)$$$. The portals $$$(1,1)$$$ and $$$(n,m)$$$ are on the north-west and south-east corner of the grid respectively.

The portal $$$(i,j)$$$ has two settings:

Type $$$t_{i,j}$$$, which is either $$$0$$$ or $$$1$$$.
Strength $$$s_{i,j}$$$, which is an integer between $$$1$$$ and $$$10^9$$$ inclusive.

Each portal has $$$4$$$ faces labelled with integers $$$0,1,2,3$$$, which correspond to the north, east, south, and west direction respectively. $\text{[math]}$

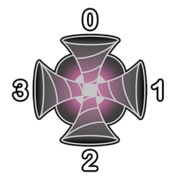
When a laser enters face $$$k$$$ of portal $$$(i, j)$$$ with speed $$$x_\text{in}$$$, it leaves the portal going out of face $$$(k+2+t_{i,j}) \bmod 4$$$ with speed $$$x_\text{out} = \max(x_\text{in},s_{i,j})$$$. The portal also has to consume $$$x_\text{out} - x_\text{in}$$$ units of energy.

Pak Chanek is very bored today. He will shoot $$$4nm$$$ lasers with an initial speed of $$$1$$$, one into each face of each portal. Each laser will travel throughout this grid of portals until it moves outside the grid or it has passed through $$$10^{100}$$$ portals.

At the end, Pak Chanek thinks that a portal is good if and only if the total energy consumed by that portal modulo $$$2$$$ is equal to its type. Given the strength settings of all portals, find a way to assign the type settings of each portal such that the number of good portals is maximised.

Input:

The first line contains two integers $$$n$$$ and $$$m$$$ ($$$1 \le n, m \le 1000$$$) — the number of rows and columns in the grid.

The $$$i$$$-th of the next $$$n$$$ lines contains $$$m$$$ integers, with the $$$j$$$-th integer being $$$s_{i,j}$$$ ($$$1 \leq s_{i,j} \leq 10^9$$$) — the strength of portal $$$(i, j)$$$.

Output:

Print $$$n$$$ lines with each line containing a string of length $$$m$$$ consisting of characters $$$0$$$ or $$$1$$$ representing the type settings. The $$$j$$$-th character in the $$$i$$$-th string is the type setting of portal $$$(i, j)$$$.

If there are multiple solutions, you can output any of them.

Sample Input:

2 3
8 8 2
6 5 7

Sample Output:

110
100

Sample Input:

1 2
420 69

Sample Output:

Note:

In the first example, let's consider the laser Pak Chanek shoots into face $$$1$$$ of portal $$$(2, 2)$$$. The laser travels as follows:

The laser enters face $$$1$$$ of portal $$$(2, 2)$$$ with speed $$$1$$$. It leaves the portal going out of face $$$3$$$ with speed $$$5$$$. Portal $$$(2, 2)$$$ consumes $$$4$$$ units of energy.
The laser enters face $$$1$$$ of portal $$$(2, 1)$$$ with speed $$$5$$$. It leaves the portal going out of face $$$0$$$ with speed $$$6$$$. Portal $$$(2, 1)$$$ consumes $$$1$$$ units of energy.
The laser enters face $$$2$$$ of portal $$$(1, 1)$$$ with speed $$$6$$$. It leaves the portal going out of face $$$1$$$ with speed $$$8$$$. Portal $$$(1, 1)$$$ consumes $$$2$$$ units of energy.
The laser enters face $$$3$$$ of portal $$$(1, 2)$$$ with speed $$$8$$$. It leaves the portal going out of face $$$2$$$ with speed $$$8$$$. Portal $$$(1, 2)$$$ consumes $$$0$$$ units of energy.
The laser enters face $$$0$$$ of portal $$$(2, 2)$$$ with speed $$$8$$$. It leaves the portal going out of face $$$2$$$ with speed $$$8$$$. Portal $$$(2, 2)$$$ consumes $$$0$$$ units of energy.

The illustration of the travel of the laser above is as follows.

$\text{[math]}$

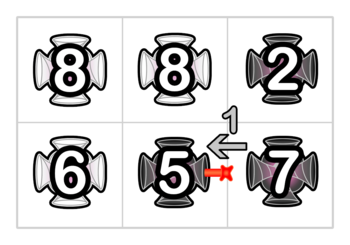
As an example, consider portal $$$(2, 3)$$$. We can calculate that the total energy consumed by that portal in the end will be $$$32$$$. Since $$$32 \bmod 2 = 0$$$ and $$$t_{2,3} = 0$$$, then it is a good portal.

Informação

Provedor Codeforces

Código CF1740G