Multi-Colored Segments

Description:

Input:

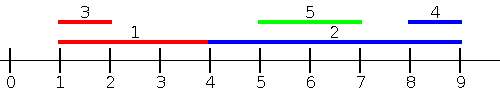
The first line of the input contains an integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases in the test.

The descriptions of the test cases follow.

The first line of description of each test case contains one integer $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — the number of segments.

The next $$$n$$$ lines contain descriptions of the segments. Each segment is described by three integers $$$l_i$$$, $$$r_i$$$ and $$$c_i$$$ ($$$1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n$$$) — coordinates of the left and right ends of $$$i$$$-th segment, as well as the color of this segment. It is guaranteed that there are at least $$$2$$$ segments of different colors.

It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.

Output:

For each test case, on a separate line print $$$n$$$ integers, where the $$$i$$$-th number is equal to the distance from the $$$i$$$-th segment to the nearest segment of a different color.

Sample Input:

9
3
1 2 1
3 4 1
5 6 2
2
100000000 200000000 1
900000000 1000000000 2
5
1 2 1
2 3 2
3 4 3
4 5 4
5 6 5
5
1 5 1
4 9 2
1 2 1
8 9 2
5 7 3
2
1 100 2
10 90 1
3
1 1 1
10 10 2
1000000000 1000000000 3
3
3 4 1
2 5 1
1 6 2
6
5 6 2
11 12 3
7 8 2
3 4 2
1 2 1
9 10 2
2
1 3 1
2 3 2

Sample Output:

3 1 1 
700000000 700000000 
0 0 0 0 0 
0 0 2 1 0 
0 0 
9 9 999999990 
0 0 0 
3 1 3 1 1 1 
0 0 

Sample Input:

4
8
11 16 7
12 15 7
2 5 8
17 22 5
1 8 8
19 23 8
16 16 6
6 7 5
9
1 4 3
5 11 1
8 11 3
1 10 1
2 11 1
1 10 4
3 11 1
5 7 1
1 11 1
9
25 25 1
26 26 1
24 24 2
13 14 2
12 16 2
17 18 1
19 19 1
24 27 2
24 27 1
9
15 18 1
20 22 2
13 22 2
13 22 2
3 13 2
6 10 2
3 6 2
19 24 2
22 24 2

Sample Output:

0 1 1 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 
0 0 0 3 1 1 3 0 0 
0 2 0 0 2 5 9 1 4 

Note:

In the first test case of the first sample there is only one segment of color $$$2$$$, and all other segments have color $$$1$$$. Therefore, for segments of color $$$1$$$, the answer is equal to the distance to the $$$3$$$rd segment, and for $$$3$$$rd one, the answer is equal to the minimum of the distances to segments of color $$$1$$$.

In the second test case of the first sample there are only $$$2$$$ segments, and for both of them the answer is equal to the distance between them.

In the third test case of the first sample, each segment intersects at least one of its ends with a segment of a different color, so all answers are equal to $$$0$$$.

The fourth test case of the first sample is described in the problem statement.

In the fifth test case of the first sample, one segment lies completely inside the other, and for both of them the answer is $$$0$$$.

In the sixth test case of the first sample, all segments are points of different colors.