Challenging Valleys

2000ms

262144K

Description:

You are given an array $$$a[0 \dots n-1]$$$ of $$$n$$$ integers. This array is called a "valley" if there exists exactly one subarray $$$a[l \dots r]$$$ such that:

$$$0 \le l \le r \le n-1$$$,
$$$a_l = a_{l+1} = a_{l+2} = \dots = a_r$$$,
$$$l = 0$$$ or $$$a_{l-1} > a_{l}$$$,
$$$r = n-1$$$ or $$$a_r < a_{r+1}$$$.

Here are three examples:

$\text{[math]}$

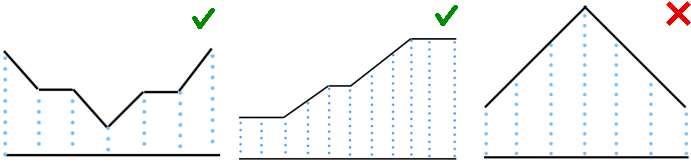
The first image shows the array [$$$3, 2, 2, 1, 2, 2, 3$$$], it is a valley because only subarray with indices $$$l=r=3$$$ satisfies the condition.

The second image shows the array [$$$1, 1, 1, 2, 3, 3, 4, 5, 6, 6, 6$$$], it is a valley because only subarray with indices $$$l=0, r=2$$$ satisfies the codition.

The third image shows the array [$$$1, 2, 3, 4, 3, 2, 1$$$], it is not a valley because two subarrays $$$l=r=0$$$ and $$$l=r=6$$$ that satisfy the condition.

You are asked whether the given array is a valley or not.

Note that we consider the array to be indexed from $$$0$$$.

Input:

The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — the number of test cases.

The first line of each test case contains a single integer $$$n$$$ ($$$1 \leq n \leq 2\cdot10^5$$$) — the length of the array.

The second line of each test case contains $$$n$$$ integers $$$a_i$$$ ($$$1 \leq a_i \leq 10^9$$$) — the elements of the array.

It is guaranteed that the sum of $$$n$$$ over all test cases is smaller than $$$2\cdot10^5$$$.

Output:

For each test case, output "YES" (without quotes) if the array is a valley, and "NO" (without quotes) otherwise.

You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).

Sample Input:

6
7
3 2 2 1 2 2 3
11
1 1 1 2 3 3 4 5 6 6 6
7
1 2 3 4 3 2 1
7
9 7 4 6 9 9 10
1
1000000000
8
9 4 4 5 9 4 9 10

Sample Output:

YES
YES
NO
YES
YES
NO

Note:

The first three test cases are explained in the statement.

Informação

Provedor Codeforces

Código CF1760D