Preparando MOJI
Let's call an ordered pair of nodes $$$(u, v)$$$ in a directed graph unidirectional if $$$u \neq v$$$, there exists a path from $$$u$$$ to $$$v$$$, and there are no paths from $$$v$$$ to $$$u$$$.
A directed graph is called $$$p$$$-reachable if it contains exactly $$$p$$$ ordered pairs of nodes $$$(u, v)$$$ such that $$$u < v$$$ and $$$u$$$ and $$$v$$$ are reachable from each other. Find the minimum number of nodes required to create a $$$p$$$-reachable directed graph.
Also, among all such $$$p$$$-reachable directed graphs with the minimum number of nodes, let $$$G$$$ denote a graph which maximizes the number of unidirectional pairs of nodes. Find this number.
The first and only line contains a single integer $$$p$$$ ($$$0 \le p \le 2 \cdot 10^5$$$) — the number of ordered pairs of nodes.
Print a single line containing two integers — the minimum number of nodes required to create a $$$p$$$-reachable directed graph, and the maximum number of unidirectional pairs of nodes among all such $$$p$$$-reachable directed graphs with the minimum number of nodes.
3
3 0
4
5 6
0
0 0
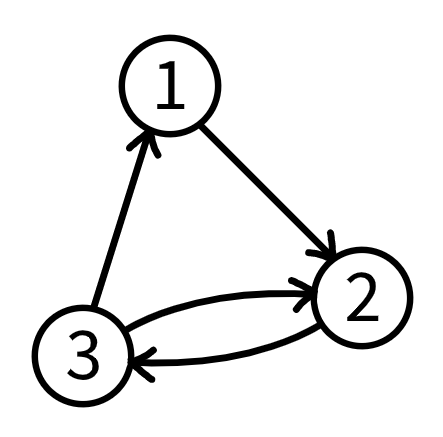
In the first test case, the minimum number of nodes required to create a $$$3$$$-reachable directed graph is $$$3$$$. Among all $$$3$$$-reachable directed graphs with $$$3$$$ nodes, the following graph $$$G$$$ is one of the graphs with the maximum number of unidirectional pairs of nodes, which is $$$0$$$.
Informação
Provedor Codeforces
Código CF1763E
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 10:34:04
Relacionados