Preparando MOJI
This is an interactive problem.
Li Ming and Li Hua are playing a game. Li Hua has a chessboard of size $$$n\times m$$$. Denote $$$(r, c)$$$ ($$$1\le r\le n, 1\le c\le m$$$) as the cell on the $$$r$$$-th row from the top and on the $$$c$$$-th column from the left. Li Ming put a king on the chessboard and Li Hua needs to guess its position.
Li Hua can ask Li Ming no more than $$$3$$$ questions. In each question, he can choose a cell and ask the minimum steps needed to move the king to the chosen cell. Each question is independent, which means the king doesn't actually move.
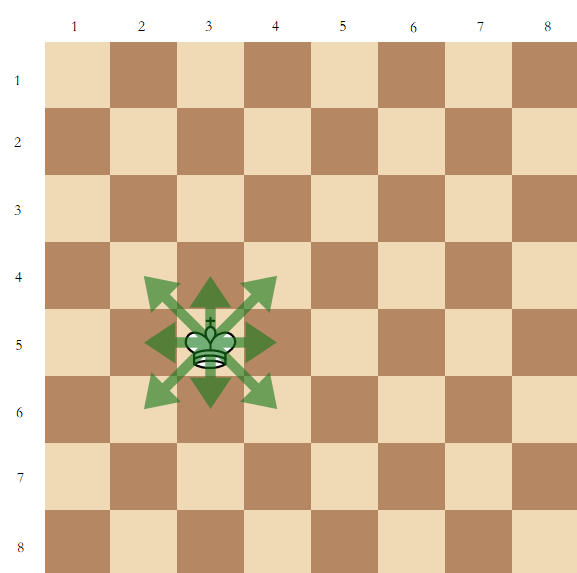
A king can move from $$$(x,y)$$$ to $$$(x',y')$$$ if and only if $$$\max\{|x-x'|,|y-y'|\}=1$$$ (shown in the following picture).
 |
The position of the king is chosen before the interaction.
Suppose you were Li Hua, please solve this problem.
The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^3$$$).
The first line of each test case contains two integers $$$n,m$$$ ($$$1\le n,m\le 10^9$$$) — the size of the chessboard, and then the interaction begins.
To ask a question, print "? $$$r$$$ $$$c$$$" (without quotes, $$$1 \leq r \leq n, 1 \leq c \leq m$$$). Then you should input the response from standard input — the minimum steps the king needs to move to the chosen cell.
If your program has asked an invalid question or has run out of questions, the interactor will terminate immediately and your program will get a verdict Wrong answer.
To give the final answer, print "! $$$r$$$ $$$c$$$" (without the quotes, $$$(r,c)$$$ is the king's initial coordinate). Note that giving this answer is not counted towards the limit of $$$3$$$ questions.
After asking a question do not forget to output the end of line and flush the output. Otherwise, you will get Idleness limit exceeded. To do this, use:
Hacks
To hack, use the following format.
The first line should contain a single integer $$$t$$$ ($$$1 \le t \le 10^3$$$).
The first and only line of each test case should contain four integers $$$n,m,r,c$$$ ($$$1\le r\le n\le 10^9,1\le c\le m\le 10^9$$$).
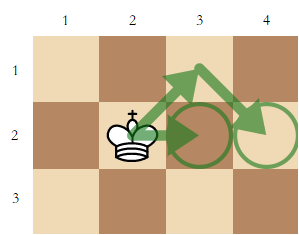
2 3 4 1 2 5 3 3 1 2
? 2 3 ? 2 4 ! 2 2 ? 2 2 ? 5 2 ? 5 3 ! 5 1
In test case 1, the king is at $$$(2,2)$$$. It takes $$$1$$$ step to move to $$$(2,3)$$$ and $$$2$$$ steps to move to $$$(2,4)$$$.
 |
Note that the questions may not seem sensible. They are just a sample of questions you may ask.