Li Hua and Tree

2000ms

262144K

Description:

Li Hua has a tree of $$$n$$$ vertices and $$$n-1$$$ edges. The root of the tree is vertex $$$1$$$. Each vertex $$$i$$$ has importance $$$a_i$$$. Denote the size of a subtree as the number of vertices in it, and the importance as the sum of the importance of vertices in it. Denote the heavy son of a non-leaf vertex as the son with the largest subtree size. If multiple of them exist, the heavy son is the one with the minimum index.

Li Hua wants to perform $$$m$$$ operations:

"1 $$$x$$$" ($$$1\leq x \leq n$$$) — calculate the importance of the subtree whose root is $$$x$$$.
"2 $$$x$$$" ($$$2\leq x \leq n$$$) — rotate the heavy son of $$$x$$$ up. Formally, denote $$$son_x$$$ as the heavy son of $$$x$$$, $$$fa_x$$$ as the father of $$$x$$$. He wants to remove the edge between $$$x$$$ and $$$fa_x$$$ and connect an edge between $$$son_x$$$ and $$$fa_x$$$. It is guaranteed that $$$x$$$ is not root, but not guaranteed that $$$x$$$ is not a leaf. If $$$x$$$ is a leaf, please ignore the operation.

Suppose you were Li Hua, please solve this problem.

Input:

The first line contains 2 integers $$$n,m$$$ ($$$2\le n\le 10^{5},1\le m\le 10^{5}$$$) — the number of vertices in the tree and the number of operations.

The second line contains $$$n$$$ integers $$$a_{1},a_{2},\ldots ,a_{n}$$$ ($$$-10^{9}\le a_{i}\le 10^{9}$$$) — the importance of each vertex.

Next $$$n-1$$$ lines contain the edges of the tree. The $$$i$$$-th line contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1\le u_i,v_i\le n$$$, $$$u_i\ne v_i$$$) — the corresponding edge. The given edges form a tree.

Next $$$m$$$ lines contain operations — one operation per line. The $$$j$$$-th operation contains two integers $$$t_{j},x_{j}$$$ ($$$t_{j}\in \{1,2\}$$$, $$$1 \leq x_{j} \leq n$$$, $$$x_{j}\neq 1$$$ if $$$t_j = 2$$$) — the $$$j$$$-th operation.

Output:

For each query "1 $$$x$$$", output the answer in an independent line.

Sample Input:

7 4
1 1 1 1 1 1 1
1 2
1 3
2 4
2 5
3 6
6 7
1 6
2 3
1 6
1 2

Sample Output:

2
3
3

Sample Input:

10 14
-160016413 -90133231 -671446275 -314847579 -910548234 121155052 -359359950 83112406 -704889624 145489303
1 6
1 10
10 8
1 4
3 4
2 7
2 5
3 2
9 8
1 4
2 2
2 4
1 4
1 10
2 10
1 9
1 6
2 8
2 10
1 5
1 8
1 1
2 5

Sample Output:

-2346335269
-314847579
-476287915
-704889624
121155052
-1360041415
228601709
-2861484545

Note:

In the first example:

The initial tree is shown in the following picture:

$\text{[math]}$

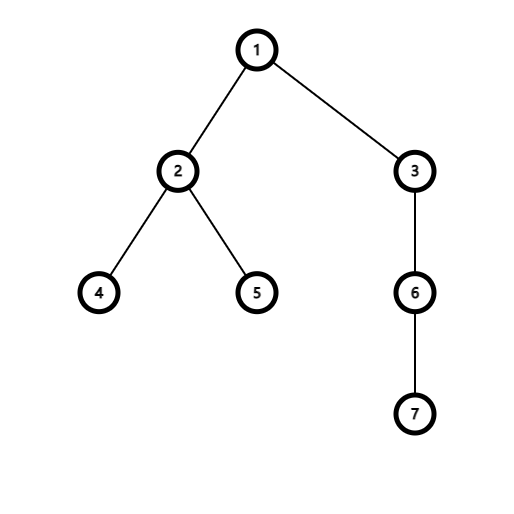The importance of the subtree of $$$6$$$ is $$$a_6+a_7=2$$$.

After rotating the heavy son of $$$3$$$ (which is $$$6$$$) up, the tree is shown in the following picture:

$\text{[math]}$

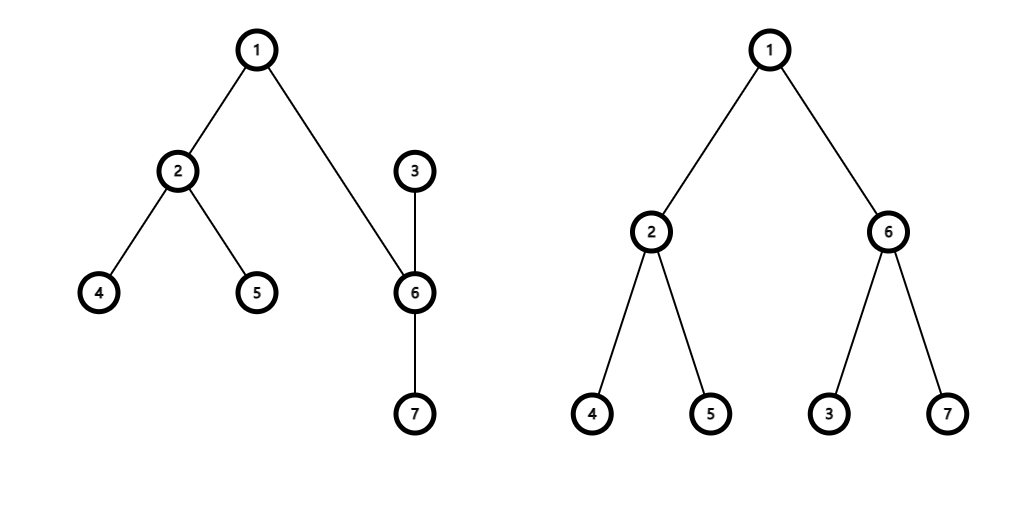The importance of the subtree of $$$6$$$ is $$$a_6+a_3+a_7=3$$$.

The importance of the subtree of $$$2$$$ is $$$a_2+a_4+a_5=3$$$.

Informação

Provedor Codeforces

Código CF1797D