LuoTianyi and XOR-Tree

Description:

Input:

The first line contains a single integer $$$n$$$ ($$$2 \le n \le 10^5$$$) — the number of vertices in the tree.

The second line contains $$$n$$$ integers $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \le a_i \le 10^9$$$), the $$$i$$$-th number represents the value in the $$$i$$$-th vertex.

Next $$$n−1$$$ lines describe the edges of the tree. The $$$i$$$-th line contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i,v_i \le n, u_i \neq v_i$$$) — the vertices connected by an edge of the tree. It's guaranteed that the given edges form a tree.

Output:

Print a single integer — the minimum number of operations.

Sample Input:

6
3 5 7 5 8 4
1 2
1 3
1 4
3 5
4 6

Sample Output:

3

Sample Input:

8
7 10 7 16 19 9 16 11
1 5
4 2
6 5
5 2
7 2
2 3
3 8

Sample Output:

3

Sample Input:

4
1 2 1 2
1 2
2 3
4 3

Sample Output:

0

Sample Input:

9
4 3 6 1 5 5 5 2 7
1 2
2 3
4 1
4 5
4 6
4 7
8 1
8 9

Sample Output:

2

Note:

The tree in the first example:

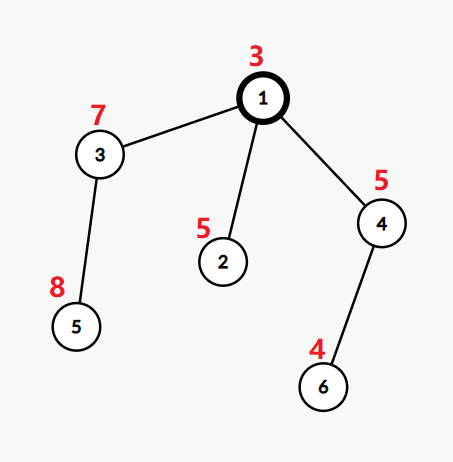
If we change the value in the vertex $$$2$$$ to $$$3$$$, the value in the vertex $$$5$$$ to $$$4$$$, and the value in the vertex $$$6$$$ to $$$6$$$, then the tree will be ok.

The bitwise XOR from the root to the leaf $$$2$$$ will be $$$3 \oplus 3=0$$$.

The bitwise XOR from the root to the leaf $$$5$$$ will be $$$4 \oplus 7 \oplus 3=0$$$.

The bitwise XOR from the root to the leaf $$$6$$$ will be $$$6 \oplus 5 \oplus 3=0$$$.

The tree in the second example:

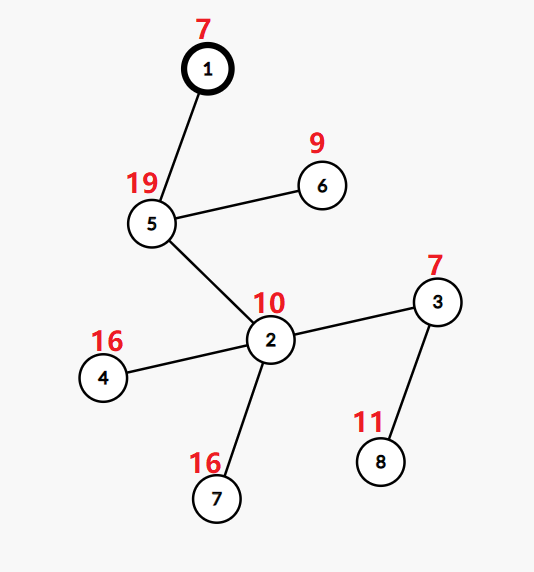
If we change the value in the vertex $$$2$$$ to $$$4$$$, the value in the vertex $$$3$$$ to $$$27$$$, and the value in the vertex $$$6$$$ to $$$20$$$, then the tree will be ok.

The bitwise XOR from the root to the leaf $$$6$$$ will be $$$20 \oplus 19 \oplus 7=0$$$.

The bitwise XOR from the root to the leaf $$$8$$$ will be $$$11 \oplus 27 \oplus 4 \oplus 19 \oplus 7=0$$$.

The bitwise XOR from the root to the leaf $$$4$$$ will be $$$16 \oplus 4 \oplus 19 \oplus 7=0$$$.

The bitwise XOR from the root to the leaf $$$7$$$ will be $$$16 \oplus 4 \oplus 19 \oplus 7=0$$$.

In the third example, the only leaf is the vertex $$$4$$$ and the bitwise XOR on the path to it is $$$1 \oplus 2 \oplus 1 \oplus 2 = 0$$$, so we don't need to change values.

In the fourth example, we can change the value in the vertex $$$1$$$ to $$$5$$$, and the value in the vertex $$$4$$$ to $$$0$$$.

Here $$$\oplus$$$ denotes the bitwise XOR operation.