LuoTianyi and Cartridge

3000ms

1048576K

Description:

LuoTianyi is watching the anime Made in Abyss. She finds that making a Cartridge is interesting. To describe the process of making a Cartridge more clearly, she abstracts the original problem and gives you the following problem.

You are given a tree $$$T$$$ consisting of $$$n$$$ vertices. Each vertex has values $$$a_i$$$ and $$$b_i$$$ and each edge has values $$$c_j$$$ and $$$d_j$$$.

Now you are aim to build a tree $$$T'$$$ as follows:

First, select $$$p$$$ vertices from $$$T$$$ ($$$p$$$ is a number chosen by yourself) as the vertex set $$$S'$$$ of $$$T'$$$.
Next, select $$$p-1$$$ edges from $$$T$$$ one by one (you cannot select one edge more than once).
May you have chosen the $$$j$$$-th edge connects vertices $$$x_j$$$ and $$$y_j$$$ with values $$$(c_j,d_j)$$$, then you can choose two vertices $$$u$$$ and $$$v$$$ in $$$S'$$$ that satisfy the edge $$$(x_j,y_j)$$$ is contained in the simple path from $$$u$$$ to $$$v$$$ in $$$T$$$, and link $$$u$$$ and $$$v$$$ in $$$T'$$$ by the edge with values $$$(c_j,d_j)$$$ ($$$u$$$ and $$$v$$$ shouldn't be contained in one connected component before in $$$T'$$$).

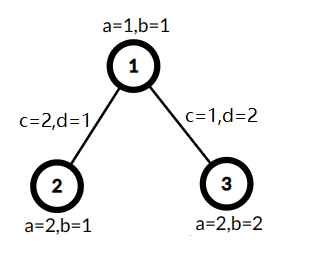$\text{[math]}$ A tree with three vertices, $$$\min(A,C)=1,B+D=7$$$, the cost is $$$7$$$. 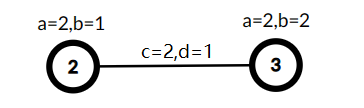$\text{[math]}$ Selected vertices $$$2$$$ and $$$3$$$ as $$$S'$$$, used the edge $$$(1,2)$$$ with $$$c_j = 2$$$ and $$$d_j = 1$$$ to link this vertices, now $$$\min(A,C)=2,B+D=4$$$, the cost is $$$8$$$.

Let $$$A$$$ be the minimum of values $$$a_i$$$ in $$$T'$$$ and $$$C$$$ be the minimum of values $$$c_i$$$ in $$$T'$$$. Let $$$B$$$ be the sum of $$$b_i$$$ in $$$T'$$$ and $$$D$$$ be the sum of values $$$d_i$$$ in $$$T'$$$. Let $$$\min(A, C) \cdot (B + D)$$$ be the cost of $$$T'$$$. You need to find the maximum possible cost of $$$T'$$$.

Input:

The first line contains one integer $$$n$$$ ($$$3\le n \le 2\cdot 10^5$$$) — the number of vertices in the tree $$$T$$$.

The second line contains $$$n$$$ integers $$$a_1, a_2, \ldots, a_n$$$ ($$$1\le a_i\le 2\cdot 10^5$$$), where the $$$i$$$-th integer represents the $$$a_i$$$ value of the $$$i$$$-th vertex.

The third line contains $$$n$$$ integers $$$b_1, b_2, \ldots, b_n$$$ ($$$1\le b_i\le 2\cdot 10^5$$$), where the $$$i$$$-th integer represents the $$$b_i$$$ value of the $$$i$$$-th vertex.

Then $$$n-1$$$ lines follow, the $$$j$$$-th of them contains four integers $$$x_j,y_j,c_j,d_j$$$ ($$$1\le x_j,y_j\le n,1\le c_j,d_j\le 2\cdot 10^5$$$) representing the edge $$$(x_j,y_j)$$$ and its values $$$c_j$$$ and $$$d_j$$$ respectively. It's guaranteed that edges form a tree.

Output:

Print a single integer — the maximum possible cost of $$$T'$$$.

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Sample Input:

6
5 7 10 7 9 4
6 9 7 9 8 5
2 1 5 1
3 2 2 4
4 3 6 3
5 1 7 4
6 5 6 8

Sample Output:

Sample Input:

5
1000 1000 1 1000 1000
1000 1000 1 1000 1000
1 2 1 1
2 3 1000 1000
3 4 1000 1000
3 5 1000 1000

Sample Output:

Note:

The tree from the first example is shown in the statement.

The tree from the second example is shown below:

$\text{[math]}$

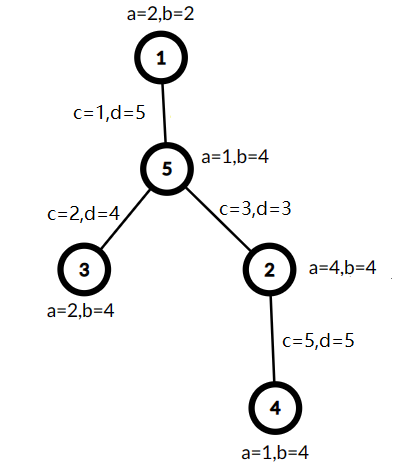
$$$A = 1, B = 18, C = 1, D = 17$$$, so the cost is $$$\min(1,1) \cdot (18 + 17) = 35$$$.

Informação

Provedor Codeforces

Código CF1824E