Preparando MOJI
This is an interactive problem.
There are $$$n$$$ distinct hidden points with real coordinates on a two-dimensional Euclidean plane. In one query, you can ask some line $$$ax + by + c = 0$$$ and get the projections of all $$$n$$$ points to this line in some order. The given projections are not exact, please read the interaction section for more clarity.
Using the minimum number of queries, guess all $$$n$$$ points and output them in some order. Here minimality means the minimum number of queries required to solve any possible test case with $$$n$$$ points.
The hidden points are fixed in advance and do not change throughout the interaction. In other words, the interactor is not adaptive.
A projection of point $$$A$$$ to line $$$ax + by + c = 0$$$ is the point on the line closest to $$$A$$$.
To query a line $$$ax + by + c = 0$$$ you should print "? a b c" where all a, b and c are real numbers up to $$$100$$$ by absolute value. For less precision issues numbers $$$a$$$ and $$$b$$$ must satisfy the condition $$$|a| + |b| \geq 0.1$$$, where $$$|a|$$$ is the absolute value of $$$a$$$.
As an answer to the query you will get $$$n$$$ points in the form "x_1 y_1 ... x_n y_n", where points $$$(x_i, y_i)$$$ are projections to the line $$$ax + by + c = 0$$$. It is guaranteed that each printed point is no more than $$$10^{-4}$$$ away from the real projection point. Every coordinate is printed with at most 9 decimal places.
See the interaction example for more clarity.
If you ask too many queries, you will get Wrong answer.
To output an answer you should print "! x_1 y_1 ... x_n y_n", where $$$(x_i, y_i)$$$ are coordinates of the hidden points. You could output the hidden points in any order. The answer would be considered correct if each of the printed points is no more than $$$10^{-3}$$$ away from the corresponding hidden point. Printing the answer doesn't count as a query.
After printing a query or the answer, do not forget to output end of line and flush the output. Otherwise, you will get Idleness limit exceeded. To do this, use:
Hacks
To make a hack, use the following test format.
In the first line output a single integer $$$t$$$ ($$$1 \leq t \leq 50$$$) — the number of test cases.
The description of the test cases follows.
In the first line of each test case output a single integer $$$n$$$ ($$$2 \leq n \leq 25$$$). In the next $$$n$$$ lines output two rational numbers each. The numbers in line $$$i$$$ should correspond to $$$x_i$$$ and $$$y_i$$$ respectively. Printed points must comply with all constraints from the input section.
The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 50$$$) — the number of test cases.
The description of the test cases follows.
The first line of each test case contains a single integer $$$n$$$ ($$$2 \leq n \leq 25$$$) — the number of hidden points.
For each test case, it is guaranteed that for any pair of hidden points, their $$$x$$$ coordinates differ by at least $$$1$$$. Analogously, $$$y$$$ coordinates of any pair also differ by at least $$$1$$$.
Coordinates $$$x$$$ and $$$y$$$ of all hidden points do not exceed $$$100$$$ by absolute value.
1 2 1 1 2.5 1 1.500000001 1.500000000 2 2
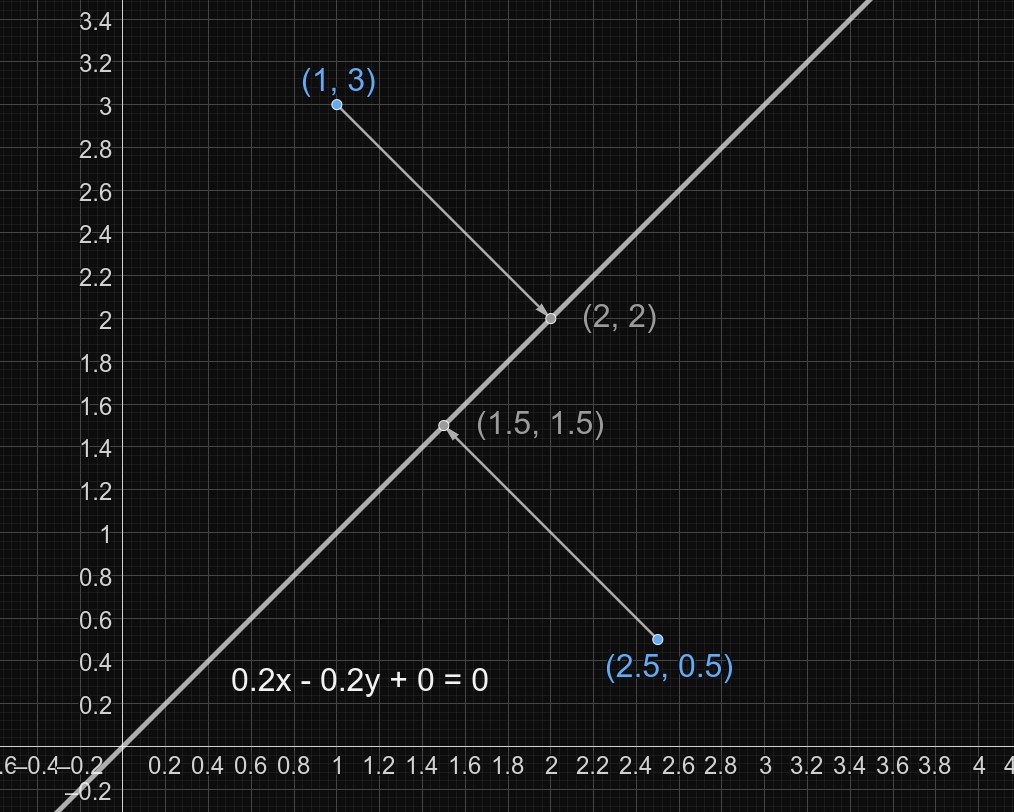
? 0 1 -1 ? 0.2 -0.2 0 ! 1 3 2.5 0.500000001
In the sample the hidden points are $$$(1, 3)$$$ and $$$(2.5, 0.5)$$$
A picture, which describes the first query:
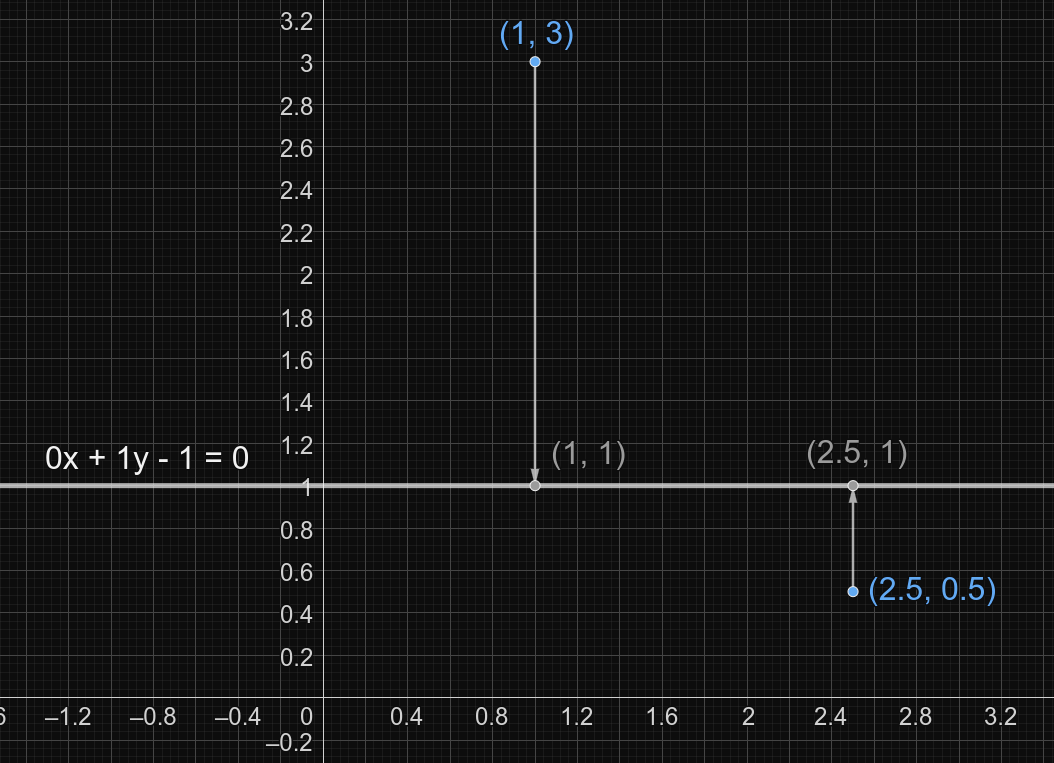
A picture, which describes the second query: