Preparando MOJI
You are given a tree (an undirected connected acyclic graph) which initially only contains vertex $$$1$$$. There will be several queries to the given tree. In the $$$i$$$-th query, vertex $$$i + 1$$$ will appear and be connected to vertex $$$p_i$$$ ($$$1 \le p_i \le i$$$).
After each query, please find out the least number of operations required to make the current tree has two centroids. In one operation, you can add one vertex and one edge to the tree such that it remains a tree.
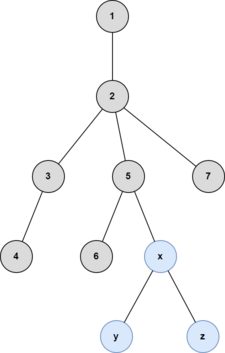
A vertex is called a centroid if its removal splits the tree into subtrees with at most $$$\lfloor \frac{n}{2} \rfloor$$$ vertices each, with $$$n$$$ as the number of vertices of the tree. For example, the centroid of the following tree is $$$3$$$ because the biggest subtree after removing the centroid has $$$2$$$ vertices.
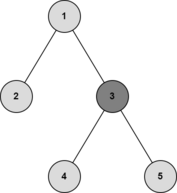
In the next tree, vertex $$$1$$$ and $$$2$$$ are both centroids.
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^4$$$). The description of the test cases follows.
The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 5 \cdot 10^{5}$$$) — the number of nodes of the final tree.
The second line of each test case contains $$$n - 1$$$ integers $$$p_1, p_2, \ldots, p_{n - 1}$$$ ($$$1 \le p_i \le i$$$) — the index of the vertex that is connected to vertex $$$i + 1$$$.
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$5 \cdot 10^{5}$$$.
For each test case, output $$$n - 1$$$ integers. The $$$i$$$-th integer is the answer to the $$$i$$$-th query — the least number of operations required to make the current tree have two centroids.
We can show that an answer always exists.
52131 141 2 371 2 3 2 5 2101 2 2 4 5 5 7 8 9
0 0 1 0 1 0 0 1 0 1 2 3 0 1 2 1 0 1 0 1 2
The illustrations below are of the fourth example test case.
After the third query:
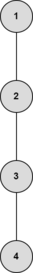
After the fourth query:
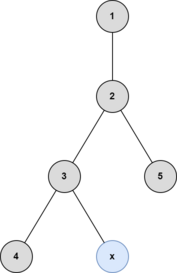
After the fifth query:
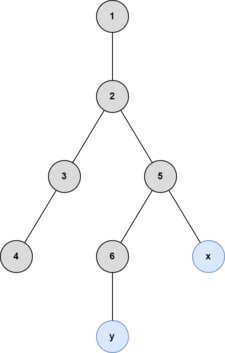
After the sixth query: