Copil Copac Draws Trees

Description:

Input:

Each test contains multiple test cases. The first line of input contains a single integer $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — the number of test cases. The description of test cases follows.

The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — the number of vertices of the tree.

The following $$$n - 1$$$ lines of each test case contain two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \neq v_i$$$) — indicating that $$$(u_i,v_i)$$$ is the $$$i$$$-th edge in the list. It is guaranteed that the given edges form a tree.

It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.

Output:

For each test case, output the number of readings Copil Copac needs to draw the tree.

Sample Input:

2
6
4 5
1 3
1 2
3 4
1 6
7
5 6
2 4
2 7
1 3
1 2
4 5

Sample Output:

2
3

Note:

In the first test case:

After the first reading, the tree will look like this:

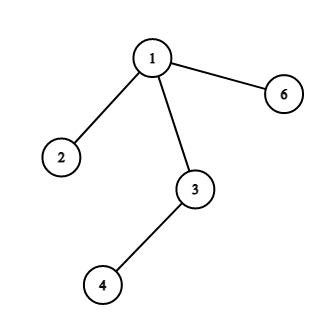
After the second reading:

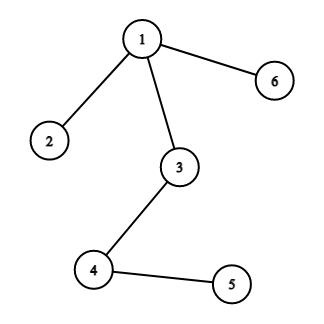
Therefore, Copil Copac needs $$$2$$$ readings to draw the tree.