Preparando MOJI
This is the hard version of the problem. The only difference is that in this version $$$n \le 10^{18}$$$.
One winter morning, Rudolf was looking thoughtfully out the window, watching the falling snowflakes. He quickly noticed a certain symmetry in the configuration of the snowflakes. And like a true mathematician, Rudolf came up with a mathematical model of a snowflake.
He defined a snowflake as an undirected graph constructed according to the following rules:
The smallest possible snowflake for $$$k = 4$$$ is shown in the figure.
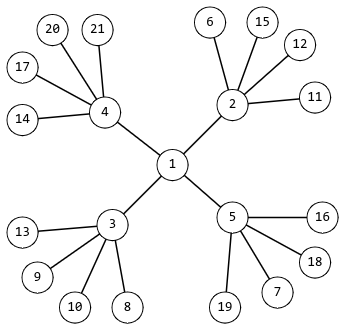
After some mathematical research, Rudolf realized that such snowflakes may not have any number of vertices. Help Rudolf check whether a snowflake with $$$n$$$ vertices can exist.
The first line of the input contains an integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases.
Then follow the descriptions of the test cases.
The first line of each test case contains an integer $$$n$$$ ($$$1 \le n \le 10^{18}$$$) — the number of vertices for which it is necessary to check the existence of a snowflake.
Output $$$t$$$ lines, each of which is the answer to the corresponding test case — "YES" if there exists such $$$k > 1$$$ that a snowflake with the given number of vertices can be constructed; "NO" otherwise.
912361315255101011000000000000000000
NO NO NO NO YES YES YES YES NO