Cardboard for Pictures

2000ms

262144K

Description:

Mircea has $$$n$$$ pictures. The $$$i$$$-th picture is a square with a side length of $$$s_i$$$ centimeters.

He mounted each picture on a square piece of cardboard so that each picture has a border of $$$w$$$ centimeters of cardboard on all sides. In total, he used $$$c$$$ square centimeters of cardboard. Given the picture sizes and the value $$$c$$$, can you find the value of $$$w$$$?

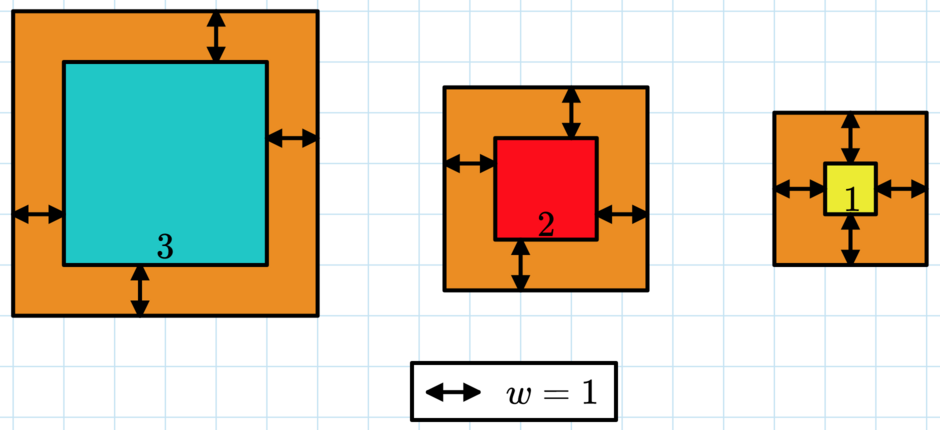$\text{[math]}$ A picture of the first test case. Here $$$c = 50 = 5^2 + 4^2 + 3^2$$$, so $$$w=1$$$ is the answer.

Please note that the piece of cardboard goes behind each picture, not just the border.

Input:

The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases.

The first line of each test case contains two positive integers $$$n$$$ ($$$1 \leq n \leq 2 \cdot 10^5$$$) and $$$c$$$ ($$$1 \leq c \leq 10^{18}$$$) — the number of paintings, and the amount of used square centimeters of cardboard.

The second line of each test case contains $$$n$$$ space-separated integers $$$s_i$$$ ($$$1 \leq s_i \leq 10^4$$$) — the sizes of the paintings.

The sum of $$$n$$$ over all test cases doesn't exceed $$$2 \cdot 10^5$$$.

Additional constraint on the input: Such an integer $$$w$$$ exists for each test case.

Please note, that some of the input for some test cases won't fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++).

Output:

For each test case, output a single integer — the value of $$$w$$$ ($$$w \geq 1$$$) which was used to use exactly $$$c$$$ squared centimeters of cardboard.

Sample Input:

10
3 50
3 2 1
1 100
6
5 500
2 2 2 2 2
2 365
3 4
2 469077255466389
10000 2023
10 635472106413848880
9181 4243 7777 1859 2017 4397 14 9390 2245 7225
7 176345687772781240
9202 9407 9229 6257 7743 5738 7966
14 865563946464579627
3654 5483 1657 7571 1639 9815 122 9468 3079 2666 5498 4540 7861 5384
19 977162053008871403
9169 9520 9209 9013 9300 9843 9933 9454 9960 9167 9964 9701 9251 9404 9462 9277 9661 9164 9161
18 886531871815571953
2609 10 5098 9591 949 8485 6385 4586 1064 5412 6564 8460 2245 6552 5089 8353 3803 3764

Sample Output:

Note:

The first test case is explained in the statement.

For the second test case, the chosen $$$w$$$ was $$$2$$$, thus the only cardboard covers an area of $$$c = (2 \cdot 2 + 6)^2 = 10^2 = 100$$$ squared centimeters.

For the third test case, the chosen $$$w$$$ was $$$4$$$, which obtains the covered area $$$c = (2 \cdot 4 + 2)^2 \times 5 = 10^2 \times 5 = 100 \times 5 = 500$$$ squared centimeters.

Informação

Provedor Codeforces

Código CF1850E