Preparando MOJI
A compass points directly toward the morning star. It can only point in one of eight directions: the four cardinal directions (N, S, E, W) or some combination (NW, NE, SW, SE). Otherwise, it will break.
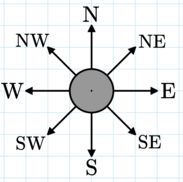 The directions the compass can point.
The directions the compass can point. There are $$$n$$$ distinct points with integer coordinates on a plane. How many ways can you put a compass at one point and the morning star at another so that the compass does not break?
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^4$$$). The description of the test cases follows.
The first line of each test case contains a single integer $$$n$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$) — the number of points.
Then $$$n$$$ lines follow, each line containing two integers $$$x_i$$$, $$$y_i$$$ ($$$-10^9 \leq x_i, y_i \leq 10^9$$$) — the coordinates of each point, all points have distinct coordinates.
It is guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$2 \cdot 10^5$$$.
For each test case, output a single integer — the number of pairs of points that don't break the compass.
530 0-1 -11 144 55 76 910 133-1000000000 10000000000 01000000000 -100000000050 02 2-1 5-1 102 1130 0-1 21 -2
6 2 6 8 0
In the first test case, any pair of points won't break the compass:
In the second test case, only two pairs of points won't break the compass: