Counting Graphs

Description:

Input:

The first line contains an integer $$$t$$$ ($$$1\le t\le 10^4$$$) — the number of test cases.

The first line of each test case contains two integers $$$n$$$ and $$$S$$$ ($$$2 \le n \le 2 \cdot 10^5, 1\le S\le 10^9$$$) — the number of vertices and the upper bound of the weights.

Then follow $$$n-1$$$ lines describing the tree, the $$$i$$$-th line contains three integers $$$u_i$$$, $$$v_i$$$, and $$$w_i$$$ ($$$1\le u_i,v_i\le n, u_i \ne v_i, 1\le w_i\le S$$$) — an edge in the tree with weight $$$w_i$$$.

It is guaranteed that the sum of $$$n$$$ for all tests does not exceed $$$2\cdot 10^5$$$.

Output:

For each test, output the number of different graphs that satisfy the conditions, modulo $$$998244353$$$.

Sample Input:

4
2 5
1 2 4
4 5
1 2 2
2 3 4
3 4 3
5 6
1 2 3
1 3 2
3 4 6
3 5 1
10 200
1 2 3
2 3 33
3 4 200
1 5 132
5 6 1
5 7 29
7 8 187
7 9 20
7 10 4

Sample Output:

1
8
80
650867886

Note:

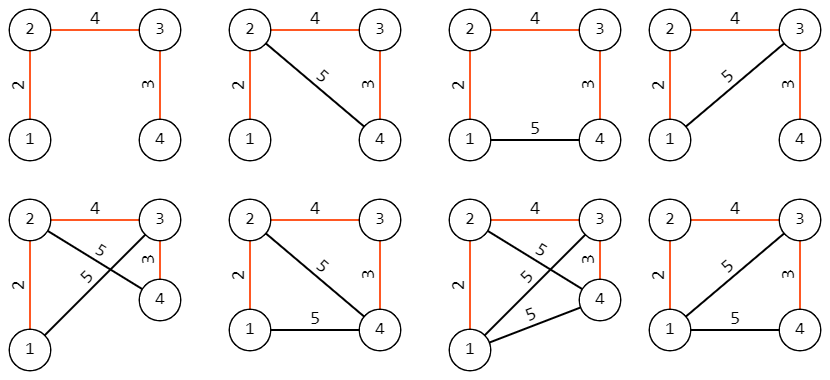
In the first sample, there is only one graph, which is the given tree.

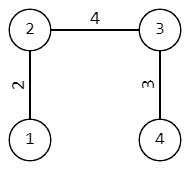
In the second samle, the given tree looks like this:

All possible graphs for the second sample are shown below, the minimum spanning tree is highlighted in red: